Hình dạng ba chiều có các mặt của nó ở dạng hình bình hành, được gọi là hình bình hành. Các diện tích hình bình hành phụ thuộc vào cơ sở (một mặt song song của nó) và chiều cao (độ cao lấy từ trên xuống dưới) của nó. Chu vi hình bình hành phụ thuộc vào độ dài bốn cạnh của nó.
Trong hình học, chắc hẳn bạn đã học về nhiều hình dạng và kích thước 2D như hình tròn, hình vuông, hình chữ nhật, hình thoi, … Tất cả các hình dạng này đều có một tập hợp các tính chất khác nhau. Ngoài ra, các công thức về diện tích và chu vi của các hình này khác nhau và được sử dụng để giải nhiều bài toán. Sau đây chúng ta cùng tìm hiểu định nghĩa, công thức và tính chất của hình bình hành.
Định nghĩa Hình bình hành
Hình bình hành là tứ giác có hai cặp cạnh đối song song. Các cạnh đối diện của hình bình hành có độ dài bằng nhau và số đo các góc đối diện bằng nhau. Ngoài ra, các góc nội thất ở cùng một bên của ngang cũng được bổ sung. Tổng của tất cả các góc bên trong bằng 360 độ.
Hình vuông và hình chữ nhật là hai hình có tính chất giống hình bình hành.
Hình thoi: Nếu tất cả các cạnh của hình bình hành bằng nhau hoặc bằng nhau thì đó là hình thoi.
Nếu có một cạnh bên song song và hai cạnh còn lại không song song thì đó là hình thang.
Xem hình bên dưới:
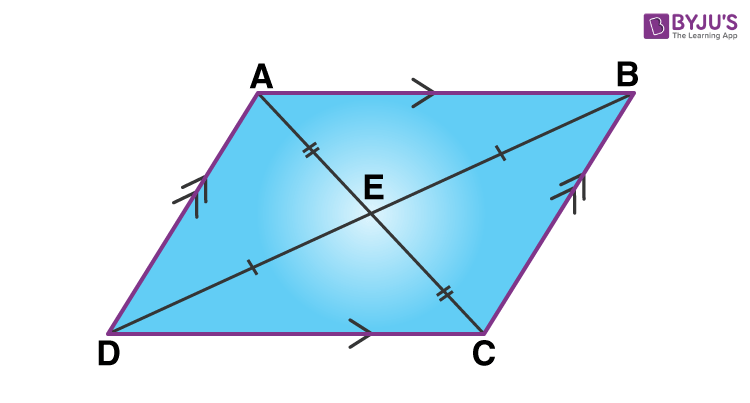
Trong hình trên, bạn có thể thấy, ABCD là hình bình hành, trong đó AB || CD và AD || BC.
Ngoài ra, AB = CD và AD = BC
Và, ∠A = ∠C & ∠B = ∠D
Ngoài ra, ∠A & ∠D là các góc bổ sung vì các góc bên trong này nằm trên cùng một phía của đường ngang. Theo cách tương tự, ∠B & ∠C là các góc phụ nhau.
Vì thế,
∠A + ∠D = 180
∠B + ∠C = 180
Hình dạng của Hình bình hành
Hình bình hành là một hình hai chiều. Nó có bốn cạnh, trong đó hai cặp cạnh song song. Ngoài ra, các cạnh song song có độ dài bằng nhau.
Nếu độ dài các cạnh của hình bình hành không bằng số đo thì hình đó không phải là hình bình hành. Tương tự, các góc đối diện của hình bình hành phải luôn bằng nhau. Nếu không, nó không phải là một hình bình hành.
Hình bình hành đặc biệt
Hình vuông và hình chữ nhật: Hình vuông và hình chữ nhật là hai hình có các tính chất giống nhau của hình bình hành. Cả hai đều có các cạnh đối diện của chúng bằng nhau và song song với nhau. Các đường chéo của cả hai hình phân giác nhau.
Hình thoi: Nếu tất cả các cạnh của hình bình hành bằng nhau hoặc bằng nhau thì đó là hình thoi.
Hình thoi: Là trường hợp đặc biệt của hình bình hành mà các cạnh đối diện của nó song song với nhau nhưng các cạnh bên có độ dài không bằng nhau. Ngoài ra, các góc bằng 90 độ.
Hình thang: Nếu có một cạnh song song và hai cạnh còn lại không song song thì đó là hình thang.
Góc của Hình bình hành
Hình bình hành là một hình phẳng 2d có bốn góc. Các góc nội thất đối diện bằng nhau. Các góc ở cùng một phía của đường ngang là bổ sung, có nghĩa là chúng cộng lại tới 180 độ. Do đó, tổng các góc trong của một hình bình hành là 360 độ.
Tính chất của Hình bình hành
Nếu một tứ giác có một cặp cạnh đối diện song song thì đó là một đa giác đặc biệt được gọi là Hình bình hành. Các tính chất của hình bình hành như sau:
- Các cạnh đối diện song song và đồng dư
- Các góc đối diện là đồng dư
- Các góc liên tiếp là phụ nhau
- Nếu ai trong số các góc là góc vuông, thì tất cả các góc khác sẽ là góc vuông
- Hai đường chéo phân giác nhau
- Mỗi đường chéo chia đôi hình bình hành thành hai tam giác đồng dạng
- Tổng bình phương tất cả các cạnh của hình bình hành bằng tổng bình phương các đường chéo của nó. Nó còn được gọi là luật hình bình hành
Ngoài ra, hãy đọc:
Công thức (Diện tích & Chu vi)
Công thức về diện tích và chu vi của một hình bình hành được đề cập ở đây trong phần này. Học sinh có thể sử dụng các công thức này và giải quyết vấn đề dựa trên chúng.
Diện tích hình bình hành
Diện tích của một hình bình hành là vùng chiếm bởi nó trong một mặt phẳng hai chiều. Dưới đây là công thức tính diện tích hình bình hành:
Diện tích = Cơ sở × Chiều cao
Trong hình trên, || gam ABCD, Diện tích được cho bởi;
trong đó a là độ dài nghiêng của cạnh || gam ABCD và b là cơ sở.
Kiểm tra ở đây: Diện tích của một công thức hình bình hành
Chu vi của Hình bình hành
Chu vi của bất kỳ hình dạng nào là tổng khoảng cách được bao phủ xung quanh hình dạng đó hoặc tổng chiều dài của hình dạng bất kỳ. Tương tự, chu vi của một hình bình hành là tổng khoảng cách của các đường biên của hình bình hành. Để tính toán giá trị chu vi, chúng ta phải biết các giá trị của chiều dài và chiều rộng của nó. Hình bình hành có độ dài các cạnh đối diện bằng nhau. Do đó, công thức tính chu vi được viết là;
Trong đó a và b là độ dài các cạnh của hình bình hành.
Các loại hình bình hành
Có chủ yếu là bốn loại hình bình hành, tùy thuộc vào các yếu tố khác nhau. Các yếu tố phân biệt tất cả các loại hình bình hành này là góc, cạnh, v.v.
- Trong một hình bình hành, giả sử PQRS
- Nếu PQ = QR = RS = SP là các cạnh bằng nhau thì đó là hình thoi. Tất cả các thuộc tính giống nhau đối với hình thoi cũng như đối với hình bình hành.
- Hai dạng đặc biệt khác của hình bình hành là:
- Hình chữ nhật
- Quảng trường
Hình vuông có phải là Hình bình hành không?
Hình vuông có thể được coi là một hình bình hành vì các cạnh đối diện song song với nhau và các đường chéo của hình vuông chia đôi nhau.
Hình chữ nhật có phải là Hình bình hành không?
Đúng, một hình chữ nhật cũng là một hình bình hành, vì nó thỏa mãn các điều kiện hoặc thỏa mãn các tính chất của hình bình hành như các cạnh đối diện là song song và các đường chéo phân giác nhau.
Định lý Hình bình hành
Định lý 1: Các hình bình hành cùng đáy và giữa các cạnh đối song song có diện tích bằng nhau.
Chứng minh: Hai hình bình hành ABCD và ABEF, trên cùng một đáy DC và nằm giữa hai đường thẳng song song AB và FC.
Để chứng minh rằng diện tích (ABCD) = diện tích (ABEF).
Bằng chứng:
Xét hình bên: Hình bình hành ABCD và hình chữ nhật ABML nằm trên cùng một đáy và nằm giữa hai cạnh AB và LC.
diện tích hình bình hành ABCD = diện tích hình bình hành ABML
Chúng ta biết rằng diện tích hình chữ nhật = chiều dài x chiều rộng.
Do đó, diện tích hình bình hành ABCD = AB x AL Do đó, diện tích hình bình hành là tích của bất kỳ đáy nào của nó và đường cao tương ứng.
Trong ∆ADF và ∆BCE,
AD = BC (∴ABCD là hình bình hành ∴ AD = BC)
AF = BE (∴ABEF là hình bình hành ∴AF = BE)
∠ADF = ∠BCE (Góc tương ứng)
∠AFD = ∠BEC (Góc tương ứng)
∠DAF = ∠CBE (Thuộc tính tổng góc)
∆ADE ≅ ∆BCF (Theo quy tắc SAS)
Diện tích (ADF) = Diện tích (BCE) (Theo tiên đề vùng đồng dư)
Diện tích (ABCD) = Diện tích (ABED) + Diện tích (BCE)
Diện tích (ABCD) = Diện tích (ABED) + Diện tích (ADF)
Diện tích (ABCD) = Diện tích (ABEF)
Do đó, diện tích các hình bình hành trên cùng đáy và giữa các cạnh đối song song bằng nhau.
Hệ quả
Một hình bình hành và một hình chữ nhật trên cùng một đáy và giữa các cạnh bằng nhau thì có diện tích bằng nhau.
Chứng minh: Vì hình chữ nhật cũng là hình bình hành nên kết quả là hệ quả trực tiếp của định lý trên.
Định lý: Diện tích hình bình hành là tích của đáy và đường cao tương ứng.
Cho: Trong hình bình hành ABCD có AB là đáy.
Để chứng minh rằng Diện tích (|| gm ABCD) = AB × AL
Cách dựng: Hoàn thành hình chữ nhật ALMB bằng cách Vẽ BM vuông góc với CD.
Sự khác biệt giữa Hình bình hành và Hình thoi
Các ví dụ đã giải quyết
Hy vọng cuộc thảo luận này đã làm rõ ràng tất cả những nghi ngờ của bạn liên quan đến Hình bình hành và các thuộc tính của chúng. Đăng ký với BYJU’S để tìm hiểu thêm về tứ giác và các khái niệm Toán học kh
