Lý thuyết Toán 8 Bài 3: Tính chất đường phân giác của tam giác
Bài giảng Toán 8 Bài 3: Tính chất đường phân giác của tam giác
A. Lý thuyết
1. Định lý
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
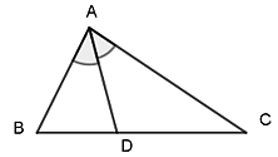

Ví dụ 1. Cho tam giác ABC có AD là đường phân giác của góc BAC^ sao cho DB = 4cm, AB = 6cm; AC = 8cm. Tính độ dài cạnh DC.
Lời giải:
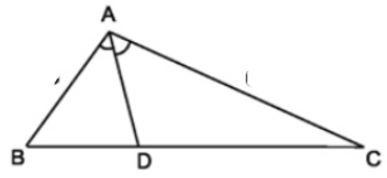
Áp dụng định lí trên ta có:
DBDC=ABAC
Hay 4DC=68⇒DC=4.86=163cm
2. Chú ý
Định lí vẫn đúng với đường phân giác của góc ngoài của tam giác
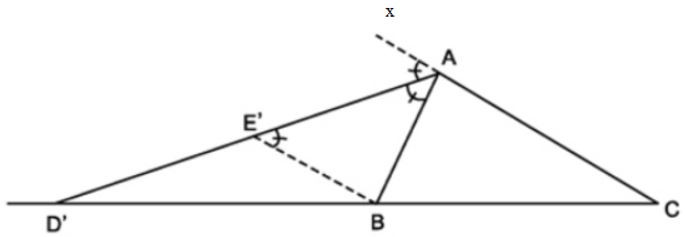
Nếu AE’ là phân giác của góc BAx^
Ta có: ABAC=DB’D’C.
B. Bài tập tự luyện
Bài 1. Cho tam giác ABC vuông tại A có AB = 6cm; BC = 10cm, AD là đường phân giác của tam giác. Tính BD; CD
Lời giải:
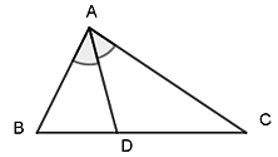
Áp dụng định lý Py – ta – go vào tam giác vuông ABC ta có:
AC2 = BC2 – AB2
nên AC=BC2-AB2=102-62=8cm
Tam giác ABC có AD là đường phân giác của góc BAC^
Ta có: DBDC=ABAC.
Khi đó ta có: DBDC=ABAC⇒DBDB+DC=ABAB+AC (tính chất tỉ lệ thức)
Hay
DB10=66+8⇒DB=307cm;DC=BC-DB=407cm
Bài 2. Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5cm.
Lời giải:
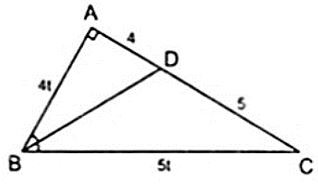
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
ABBC=DADC=45⇒AB4=BC5
Đặt AB4=BC5= t ( t > 0)
⇒AB=4tBC=5t
Áp dụng định lý Py – ta – go vào tam giác ABC ta có:
BC2 = AC2 + AB2 hay (5t)2 = 92 + (4t)2
⇔9t2 = 81.t2 = 9 nên t = 3 ( vì t > 0)
Khi đó: AB = 4.3 = 12 cm; BC = 5.3 = 15 cm
Bài 3. Cho tam giác ABC, các đường phân giác BD và CE. Biết ADDC=23, EAEB=56. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
Lời giải:
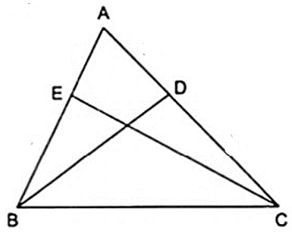
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
ABBC=ADDC=23=46⇒AB4=BC6=t⇒AB=4tBC=6tACBC=AEEB=56⇒AC5=BC6=t⇒AC=5tBC=6t
Theo giả thiết ta có, chu vi tam giác ABC là 45 nên:
AB + BC + AC = 15t = 45 nên t = 3.
Vậy AB = 12 cm; BC = 18cm; AC = 15cm.
Bài 4. Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAC^. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BMBD.
Lời giải:
Do M là trung điểm của BC nên:
BM=MC=12BC=12.15=7,5cm
Theo tính chất tia phân giác của góc ta có: ABAC=DBDC
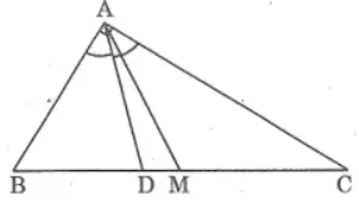
Suy ra: ABDB=ACDC
Theo tính chất của dãy tỉ số bằng nhau ta có:
ABDB=ACDC=AB+ACDB+DC=12+815=43
Suy ra:
ABBD=43⇒BD=3.AB4=3.124=9cm
Do đó: BMBD=7,59=56
Trắc nghiệm Toán 8 Bài 3: Tính chất đường phân giác của tam giác
Bài 1: Hãy chọn câu đúng. Tỉ số xy của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.
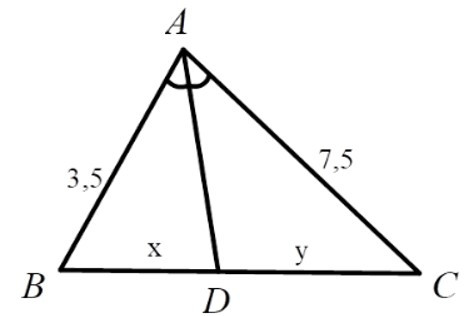
A. 715
B. 17
C. 157
D. 115
Bài 2: Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE.
1. Chọn khẳng định đúng.
A. DE // BC
B. DI = IE
C. DI > IE
D. Cả A, B đều đúng
2. Tính độ dài DE, biết BC = 30cm, AM = 10cm.
A. 9cm
B. 6cm
C. 15cm
D. 12cm
Bài 3: Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức S = 49×2 + 98y2.
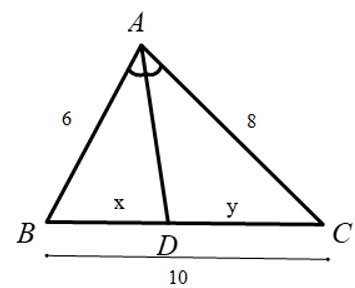
A. 3400
B. 4900
C. 4100
D. 3600
Bài 4: Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Tính BI?
A. 9cm
B. 6cm
C. 45cm
D. 35cm
Bài 5: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:
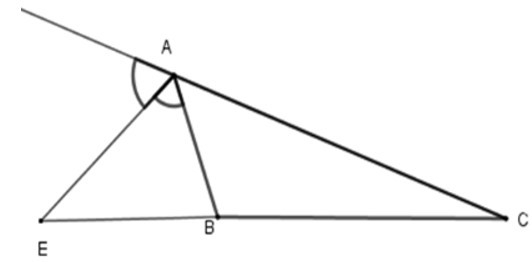
Bài 6: Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Độ dài AI là:
A. 9cm
B. 6cm
C. 45cm
D. 3 cm
Bài 7: Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:
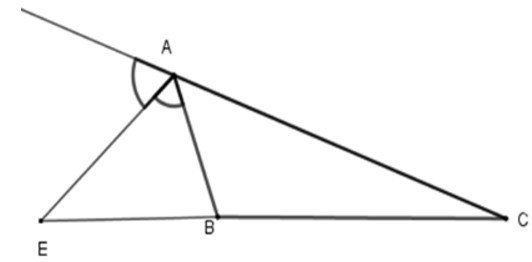
Bài 8: Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
A. 3cm
B. 6cm
C. 9cm
D. 12cm
Bài 9: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:
A. 1,5
B. 3
C. 4,5
D. 4
Bài 10: Cho tam giác ABC, A^ = 900, AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của HAB^ cắt HB tại D. Tia phân giác của HAC^ cắt HC tại E. Tính HE?
A. 4cm
B. 6cm
C. 9cm
D. 12cm
Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:
Lý thuyết Khái niệm tam giác đồng dạng
Lý thuyết Trường hợp đồng dạng thứ nhất
Lý thuyết Trường hợp đồng dạng thứ hai
Lý thuyết Trường hợp đồng dạng thứ ba
Lý thuyết Các trường hợp đồng dạng của tam giác vuông
