Công thức toán học luôn là vấn đề nan giải cho chúng ta khi còn ngồi trên ghế nhà trường. Có hàng chục thậm chí là hàng trăm loại phép tính khác nhau khiến cho đầu óc của chúng ta quay cuồng đặc biệt là bài tập về tính thể tích của khối tứ diện đều. Nhưng cũng đừng lo vì bài viết dưới đây sẽ ôn tập cho bạn lại các kiến thức về khối tứ diện đều và công thức tính thể tích khối tứ diện đều cạnh a. Đừng bỏ lỡ qua chúng nhé, vì có rất nhiều kiến thức, cũng như ví dụ thực tế dành bổ ích dành cho bạn.
Khối tứ diện đều là gì?
Khối tứ diện là gì?
Có khối tứ diện hoặc khối tứ diện đều mới nảy sinh ra các công thức tính diện tích tứ diện, tính thể tích khối tứ diện đều,…
Tứ diện được xem là hình có bốn đỉnh, thông thường hình tứ diện sẽ được kí hiệu bằng A, B, C, D. Ở bất kì điểm nào nằm trong số những điểm được nêu trên thì được là đỉnh, còn mặt tam giác sẽ đối diện với đỉnh của tứ diện được gọi là đáy.
Ví dụ: Nếu như chọn A là đỉnh thì BCD sẽ là mặt đáy. Khi vẽ hình khối tứ diện đều cũng nên lưu ý là vẽ mặt đáy BCD trước.
Khối tứ diện đều là gì?
Để nắm hiểu được công thức thể tích khối tứ diện đều thì trước tiên ta phải tìm hiểu kỹ khái niệm khối tứ diện đều là gì?
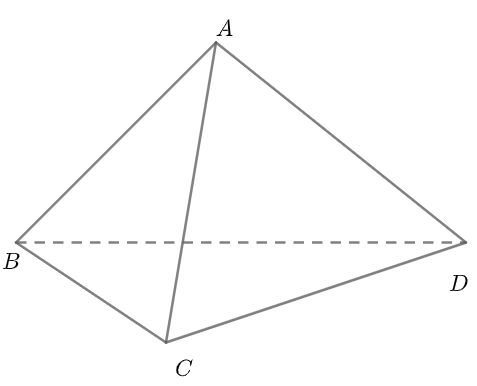
Khối tứ diện đều
Tứ diện đều là hình tứ diện bao gồm 4 mặt là tam giác đều.
Tứ diện đều được cho là một hình chóp tam giác đều.
Hình chóp tam giác đều còn có thêm các điều kiện như sau: cạnh bên sẽ bằng với cạnh đáy là tứ diện đều.
Tham khảo thêm các công thức khác :
- Công thức tính thể tích khối tròn xoay chuẩn SGK và 5 ví dụ
- Công thức tính chu vi và diện tích lục giác đều chuẩn SKG
- Công thức tính diện tích và thể tích hình cầu chuẩn SGK
- Công thức tính thể tích khối lăng trụ kèm ví dụ hay
Tính chất của khối tứ diện đều là gì?
Khối tứ diện đều sẽ có những tính chất như sau:
- Bốn mặt bao xung quanh được xem là những tam giác đều bằng với nhau.
- Các mặt của khối tứ diện là những hình tam giác có ba góc nhọn.
- Tổng các góc nằm tại một đỉnh ở bất kì của hình tứ diện là 180.
- Hai cặp cạnh mà đối diện như ở trong cùng một tứ diện đều có độ dài bằng nhau.
- Tất cả các mặt của khối tứ diện đều có kích thước tương đương nhau.
- Bốn đường cao của khối tứ diện đều có kích thước bằng nhau.
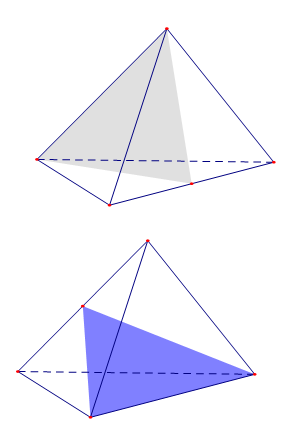Các mặt của khối tứ diện là những hình tam giác có ba góc nhọn
- Tâm của những mặt cầu ngoại tiếp và nội tiếp nhau, trùng với tâm điểm của hình tứ diện.
- Hình hộp được ngoại tiếp với khối tứ diện là hình hộp chữ nhật.
- Những góc phẳng nhị diện sẽ ứng với mỗi cặp cạnh đối diện trong khối tứ diện bằng nhau.
- Đoạn thẳng được nối với trung điểm của các cạnh đối diện sẽ là một đường thẳng đứng 90 độ (vuông góc) của cả 2 cạnh đó.
- Một tứ diện sẽ có 3 trục đối xứng.
- Tổng hết các cos của những góc phẳng nhị diện sẽ chứa cùng với một mặt của khối tứ diện bằng 1.
Nắm rõ những tính chất này để phân biệt được đâu là khối tứ diện đều và áp dụng công thức tính diện tích, thể tích khối tứ diện đều một cách chính xác nhất.
Vẽ khối tứ diện đều như thế nào?
Thông thường khi làm các bài liên quan đến tính toán thì điều đầu tiên sẽ là vẽ hình hoặc làm tóm tắt đề bài. Đối với bài tập liên quan đến thể tích khối tứ diện đều cũng vậy, phải vẽ hình mới đưa ra kết quá đúng đắn.
Những bước vẽ khối tứ diện đều như sau:
- Bước 1: đầu tiên bạn hãy xem rằng khối tứ diện đều chính là một hình chóp của tam giác đều ABCD.
- Bước 2: khi tiến hành vẽ mặt đáy cho hình. Thì cạnh đáy sẽ là mặt BCD.
- Bước 3: bước tiếp theo mà bạn cần phải tiến hành là vẽ một đường trung tuyến nằm tỏng mặt đáy BCD. Ví dụ như: đường trung tuyến có tên BM.
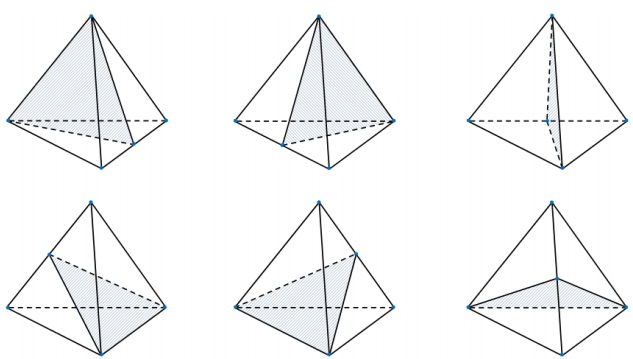Vẽ khối tứ giác đều cho thật chính xác
- Bước 4: sau đó bạn sẽ tiến hành xác định lại trọng tâm G của hình tam giác BCD.
- Bước 5: thông qua những bước trên, thì hãy đến bước tiến hành dựng đường cao.
- Bước 6: cuối cùng xác định được điểm A nằm trên đường cao vừa dựng được và hoàn thiện khối tứ diện đều.
Công thức tính thể tích khối tứ diện đều là gì?
Một khối tứ diện đều sẽ bao gồm sáu cạnh bằng nhau và bốn mặt tam giác đều. Suy ra công thức tính thể tích khối tứ diện đều sẽ được tính như sau:
Thể tích khối tứ diện đều ABCD là gì?
Thể tích khối tứ diện đều ABCD chỉ bằng được một phần ba tích số của cả diện tích mặt đáy và chiều cao của hình tứ diện tương tự:
Công thức tính thể tích như sau:
Chú thích:
- V chính là thể tích khối tứ diện đều
- SABCD chính là diện tích mặt đáy
- AH chính là chiều cao của khối tứ diện đều
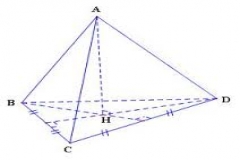
Lấy một phần ba diện tích mặt đáy nhân với đường cao
Thể tích khối tứ diện đều tam giác S.ABC là gì?
Thể tích khối tứ diện đều tam giác S.ABC sẽ bao gồm một khối hình chóp bằng được một phần ba tích số của cả diện tích mặt đáy và tổng chiều cao của khối chóp đó.
Công thức tính thể tích như sau:
Chú thích:
- V chính là thể tích khối tứ diện đều
- h chính là chiều cao của khối tứ diện đều
Bài tập áp dụng cho công thức tính thể tích khối tứ giác đều:
Hãy làm thật nhiều bài tập để ghi thật kỹ công thức tính thể tích khối tứ giác đều nhé. Mỗi hình sẽ bao gồm các phép tính khác nhau và toán hình hay toán số đều có độ khó cho riêng mình.
Chỉ có thực hành mới có thể ghi nhớ được hết lý thuyết. Nếu như chỉ học vẹt mà không chịu làm bài tập thì bạn mãi sẽ không khá lên được. Bởi vì toán học cần độ chính xác cao, phải áp dụng công thức mới cho ra kết quả chính xác nhất.
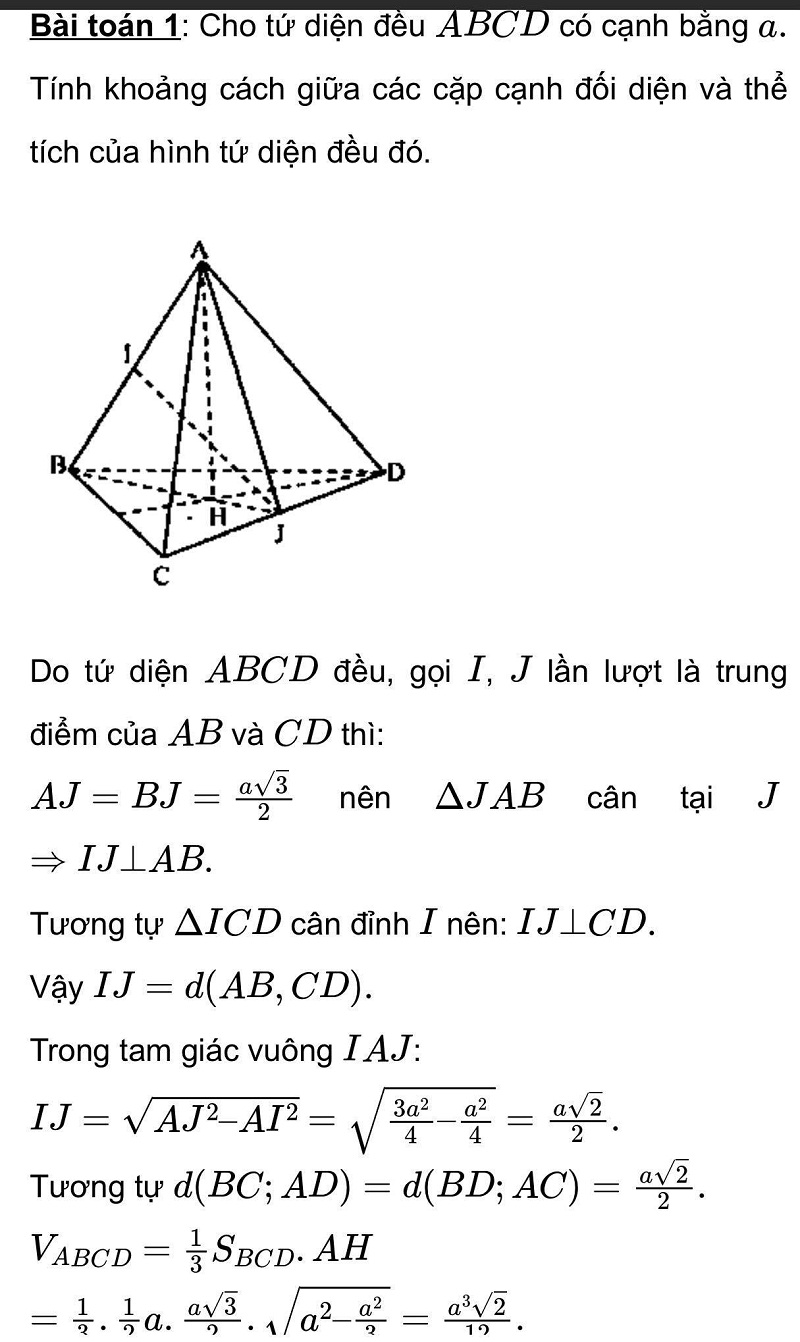
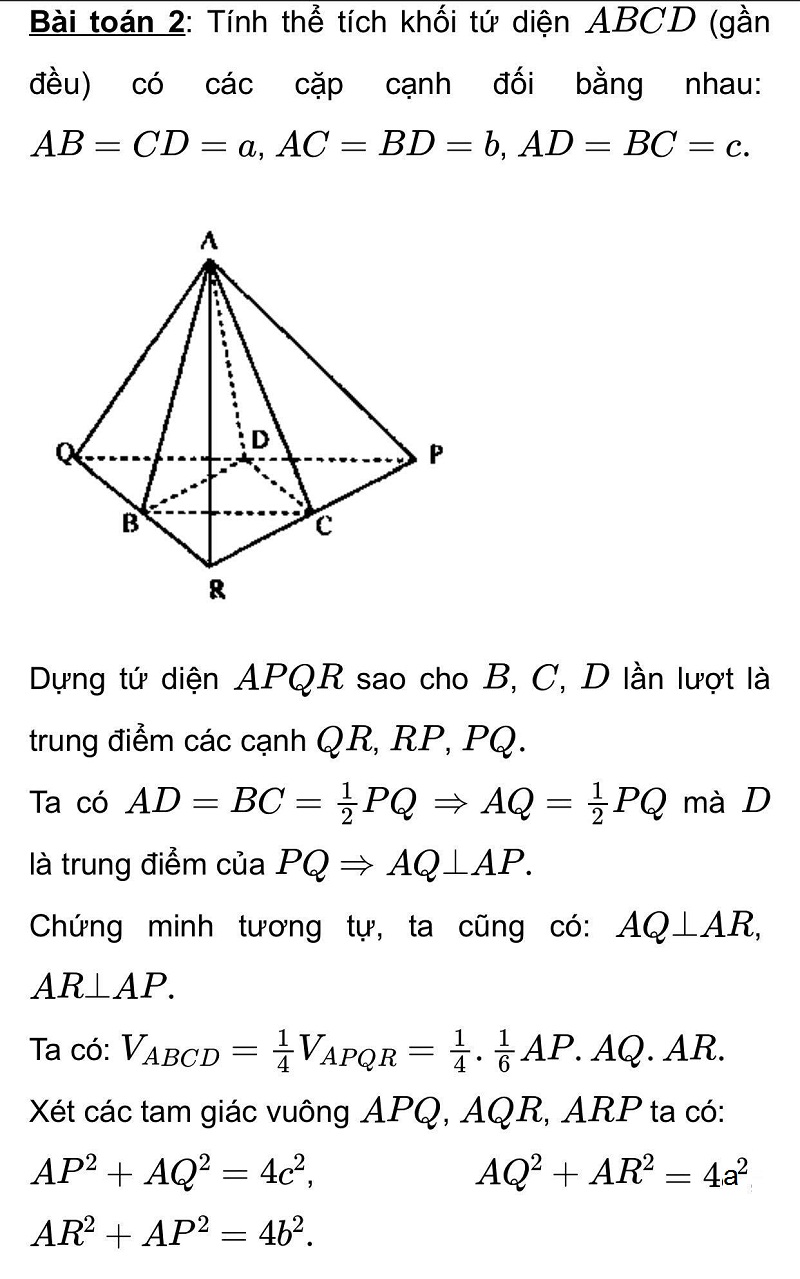
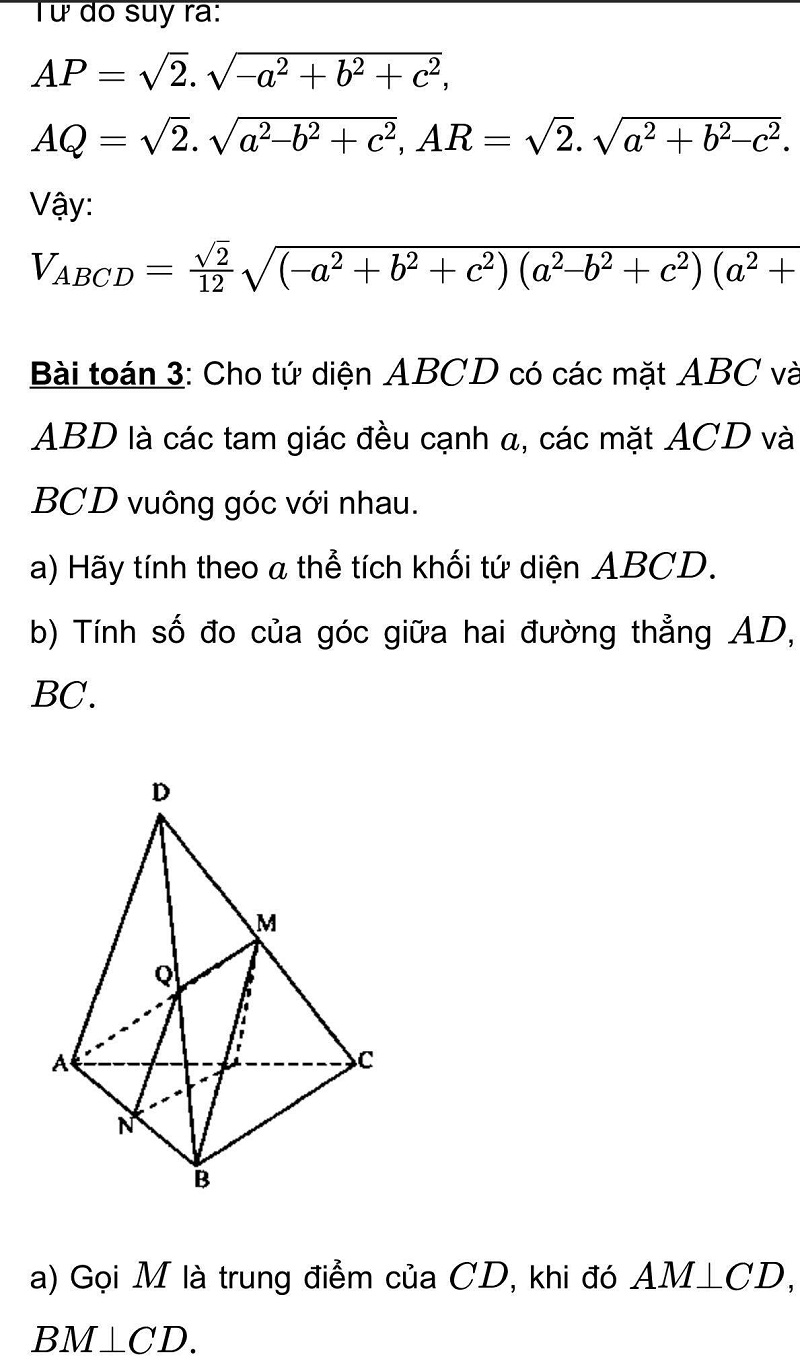
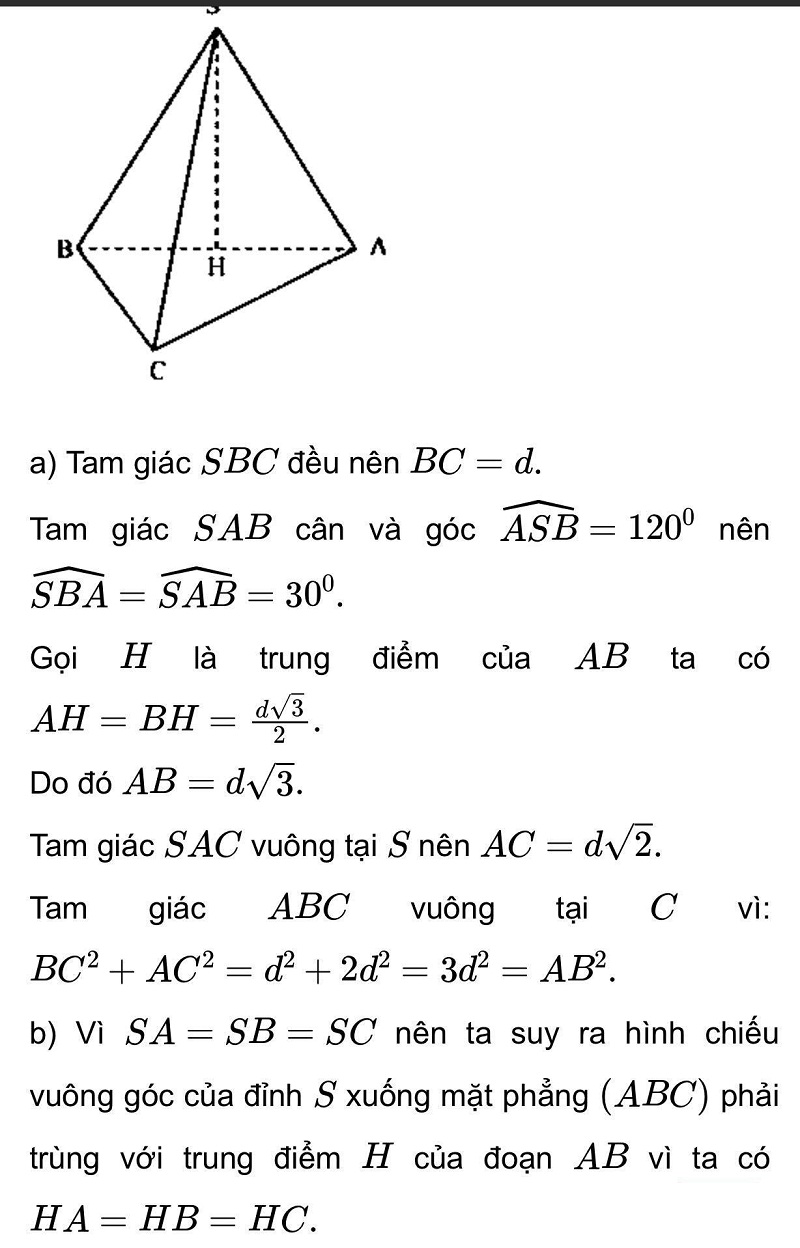
Đồng thời toán học giúp chúng ta mở rộng nguồn kiến thức, tập cho ta những kỹ năng về tư duy, phân tích vấn đề một cách thật logic. Toán học đòi hỏi độ tỉ mỉ vô cùng cao, những ai học tốt môn toán thì suy ra bộ não của họ cũng không tầm thường.
Khi gặp bài toán khó nhằn thì ta sẽ có sản sinh ra những lập luận phức tạp, điều này khiến cho bộ não của chúng ta đang hoạt động nhiệt huyết, vặn hết công suất để đem ra mọi luận cứ nghe hợp tình hợp lý. Xây dựng một hệ thống suy nghĩ bền bĩ và rành mạch, sẵn sàng phản bác những điều phi logic.
Trường hợp nào nên lưu ý khi áp dụng các công thức tính khối tứ diện đều?
Khi sử dụng phép tính thể tích khối tứ diện đều hay tính những phép tính khác liên quan đến hình khối tứ diện đều phải cần chú ý các điều như sau:
- Khối tứ diện hoặc hình chóp tam giác đều có cách chọn đỉnh chóp.
- Khối tứ diện sẽ nội tiếp với hình hộp và khối tứ diện gần đều (có những cặp cạnh đối bằng nhau) sẽ nội tiếp với hình hộp chữ nhật, cuối cùng khối tứ diện đều sẽ nội tiếp hình lập phương. Mỗi một loại hình sẽ được nối tiếp với từng khối hình khác nhau.
- Khi tính toán những đại lượng, nếu cần thiết thì ta sẽ đặt ẩn rồi đi tìm phương trình để có thể giải ra ẩn đó. Làm như vậy để ta có thể tìm ra những kết quả hợp lý nhất cho bài toán.
- Để tính được diện tích hay thể tích khối tứ diện đều thì có khi ta phải tính theo cách gián tiếp bằng việc chia nhỏ các phần hay lấy đi phần lớn hơn rồi trừ với phần dư.
Những chú ý trên sẽ giúp chúng ta hoàn thiện bài toán một cách đúng đắn hơn. Hãy rèn luyện tư duy phân tích và kỹ năng lập luận sắc bén thông qua bộ môn này nhé. Bởi vì chúng sẽ giúp ích cho các bạn không chỉ khi ngồi trên ghế nhà trường, mà chúng còn phổ biến trong đời sống xã hội hiện nay.
