Khối đa diện là gì? Bài viết dưới đây chúng ta cùng nhau đi tìm hiểu khái niệm về khối đa diện và các kiến thức liên quan. Hãy cùng theo dõi nhé!
I. HÌNH ĐA DIỆN LÀ GÌ
Hình đa diện gồm hữu hạn các đa giác phẳng thỏa mãn hai điều kiện sau:
- Điều kiện 1: Với hai đa giác bất kỳ chỉ xảy ra một trong các trường hợp sau: Không có điểm chung; Có một đỉnh chung; Có 1 cạnh chung. Có nghĩa là hình có 2 đa giác mà không thuộc 3 trường hợp trên hoặc có nhiều hơn 1 trường hợp trong ba trường hợp trên đều không thỏa mãn.
Ví dụ:
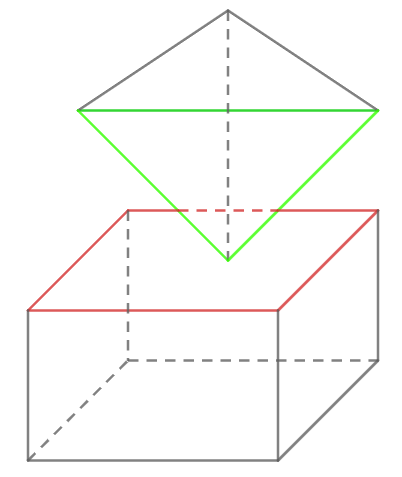
Hình trên không phải là hình biểu diễn của một hình đa dιện vì tam giác (màu xanh) và hình chữ nhật (màu đỏ) không thỏa mãn điều kiện 1. Cụ thể là 2 đa giác này có 1 điểm chung nhưng điểm chung đó lại không phải đỉnh chung.
- Điều kiện 2: Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Nghĩa là có 1 cạnh của đa giác không là cạnh chung của 2 đa giác hoặc là cạnh chung của 3 đa giác trở lên đều vi phạm.
Ví dụ:
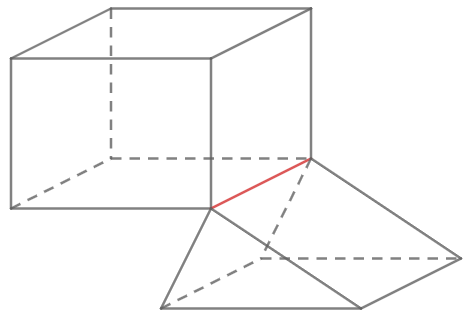
Hình trên không phải hình biểu diễn của hình đa dιện. Vì có 1 cạnh (màu đỏ) là cạnh chung của tới 4 mặt.
Các hình đa diện thường gặp mà chúng ta đã biết từ lớp 11 như: Hình tứ diện, hình chóp, hình lăng trụ, hình chóp cụt, hình hộp, hình lập phương…
II. KHỐI ĐA DIỆN LÀ GÌ
Mỗi hình đa diện chia không gian thành miền trong và miền ngoài. Hình đa diện và miền trong của nó tạo thành khối đa diện. Hay nói cách khác mỗi hình đa diện có 1 khối đa diện tương tương ứng. Ví dụ khối tứ diện, khối chóp, khối lăng trụ, khối chóp cụt, khối hộp, khối lập phương… là các khối đa diện.
Khối đa diện được phân chia làm hai loại: Khối đa diện lồi và khối đa diện không lồi. Tuy nhiên trong chương trình THPT, chúng ta chỉ nghiên cứu khối đa diện lồi.
Khối đa diện lồi là khối đa diện mà đoạn thẳng nối 2 điểm bất kỳ thuộc khối đa diện thì nằm hoàn toàn trên khối đa diện đó.
Ví dụ: Khối chóp, khối lăng trụ là các khối đa diện lồi.
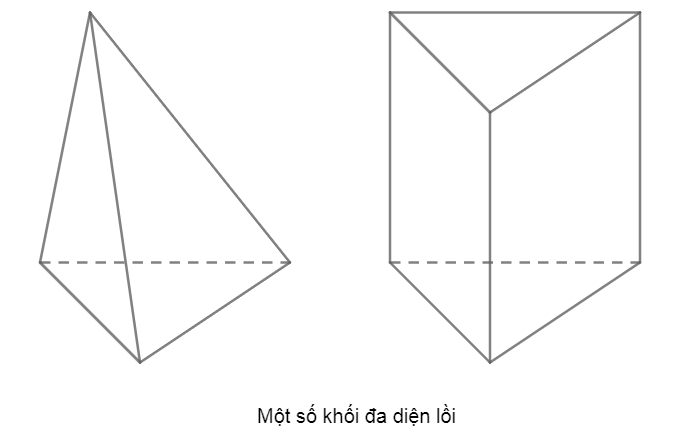
Ví dụ:
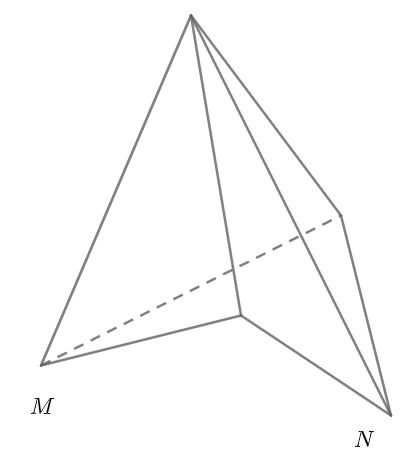
Hình trên không phải khối đa dιện lồi vì đoạn thẳng MN không nằm trên khối đa dιện.
III. KHỐI ĐA DIỆN ĐỀU LÀ GÌ
Trong số các khối đa diện lồi, chúng ta có 1 loại khối đa diện đặc biệt. Đó là khối đa diện đều.
Khối đa diện đều là khối đa diện thỏa mãn 2 điều kiện sau:
- Mỗi mặt là đa giác đều p cạnh.
- Mỗi đỉnh là đỉnh chung của đúng q mặt.
Khối đa diện như vậy được gọi là khối đa diện đều loại {p,q}. Và người ta cũng chứng minh được chỉ có đúng 5 loại khối đa diện đều (lồi).
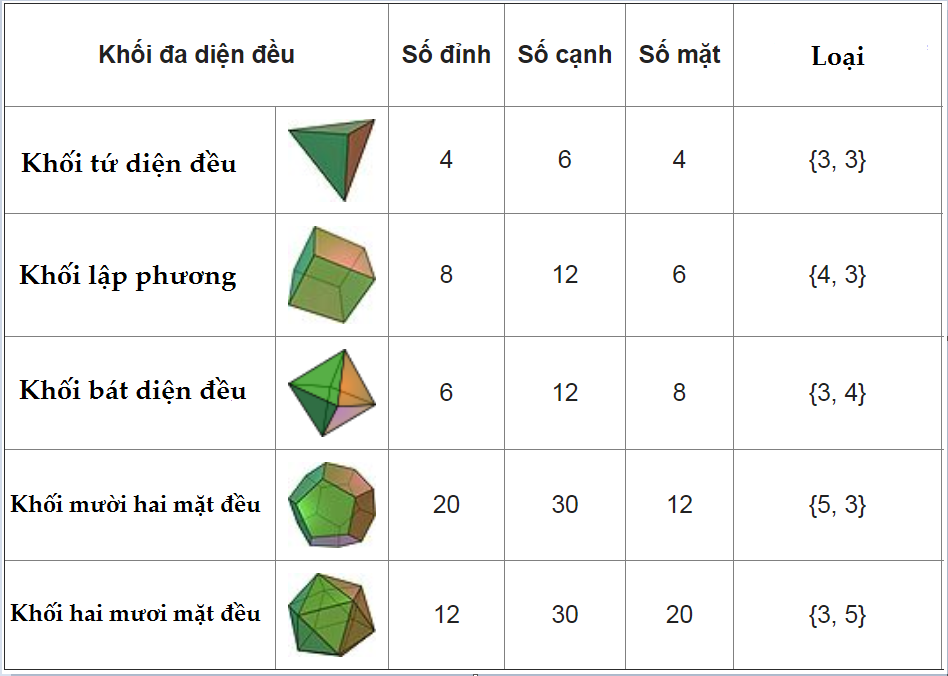
Trên đây là tổng quan về hình đa diện và khối đa diện mà toanthaydinh.com giới thiệu đến các bạn. Hãy đón đọc các bài viết tiếp theo để tìm hiểu thêm nhé. Chúc các bạn thành công!
Xem thêm:
Công thức tính thể tích khối chóp lăng trụ
Bát diện đều: Công thức tính thể tích và bài tập
Công thức tính nhanh tỉ số thể tích khối đa diện
Mặt phẳng đối xứng của các khối hình thường gặp
Thể tích tứ diện đều: Khái niệm, công thức và bài tập chi tiết






