Các dạng toán liên quan đến đồ thị hàm số như tìm và biện luận số giao điểm của 2 đồ thị hàm số, Biện luận số nghiệm của phương trình bằng đồ thị, phương trình tiếp tuyến của đồ thị đòi hỏi sự vận dụng linh hoạt của các em, dưới đây là một số dạng toán cơ bản.
* Cơ bản có 3 dạng toán liên quan tới khảo sát hàm số là:
– Dạng 1: Biện luận số giao điểm của 2 đường
– Dạng 2: Biện luận bằng đồ thị số nghiệm của phương trình
– Dạng 3: Tìm phương trình tiếp tuyến của đồ thị
* Bài toán 1: Biện luận số giao điểm của 2 đường
_ Phương pháp chung:
+ Trong mặt phẳng (Oxy) hãy xét sự tương giao của đồ thị hai hàm số: y = f(x) có đồ thị (C1) và y = g(x) có đồ thị (C2).
+ Số giao điểm của (C1) và (C2) là số nghiệm của phương trình hoành độ giao điểm f(x)= g(x) (1). Khi đó,bài toán quy về việc biện luận số nghiệm của phương trình (1). Thông thường :
– Nếu (1) là phương trình trùng phương thì quy về phương trình bậc 2
– Nếu (1) là phương trình bậc 3 hoặc bậc cao thì ta có thể hướng đến
_ Nếu cô lập được m đưa (1) thành: F(x) = h(m) thì bài toán quy về khảo sát hàm số y=F(x)
_ Nếu phương trình có nghiệm x=x0 thì đưa (1) thành: (x − x0)h(x,m) = 0 và tiếp tục biện luận với phương trình h(x,m)=0
Ví dụ 1: Cho hàm số y = (m + 1) x4 − 4×2 + 1 (C). Tìm m để (C) cắt trục hoành tại:
a) Ít nhất một điểm
b) Bốn điểm phân biệt
* Lời giải:
Phương trình hoành độ giao điểm của (C) và trục hoàng là nghiệm của phương trình:
(m + 1) x4 − 4×2 + 1 = 0 (1)
Đặt t= x2, t≥0 phương trình trở thành
(m + 1) t2 − 4t + 1 = 0 (2)
a) Đồ thị (C) cắt trục hoành tại ít nhất một điểm khi và chỉ khi phương trình (1) cónghiệm <=> phương trình (2) có nghiệm không âm.
Với m=-1 , phương trình (2) trở thành −4t + 1 = 0 ⇔ t = (1/4) > 0(thỏa mãn)
Với m ≠ -1 thì phương trình (2) là phương trình bậc 2, ta xét ba trường hợp sau:
– Trường hợp 1 : (2) có hai nghiệm không âm:
– Trường hợp 2 : phương trình (2) có hai nghiệm trái dấu: khi và chỉ khi P<0 <=> 1/(m+1)<0 <=> m<-1
– Trường hợp 3 : phương trình (2) có một nghiệm bằng 0 và một nghiệm âm (không xảy ra vì t=0 không là nghiệm của phương trình (2) với mọi m).
Vậy m ≤ 3 là giá trị cần tìm (khi đó (C) cắt trục hoành tại ít nhất 1 điểm)
b) Đồ thị (C) cắt trục hoành tại bốn điểm phân biệt <=> phương trình (1) có 4 nghiệm khác 0 <=> phương trình (2) có 2 nghiệm dương phân biệt_ Với m= -1 dễ thấy không thỏa mãn (Phương trình (2) chỉ có 1 nghiệm dương)
_ Với m ≠ -1 thì phương trình (2) là phương trình bậc 2
Phương trình (2) có hai nghiệm dương khi và chỉ khi:
Kết luận: Vậy với -1<m<3 thì (C) cắt trục hoành tại bốn điểm.
* Bài toán 2: Biện luận bằng đồ thị số nghiệm của phương trình:
– Cho phương trình F(x, m) = 0 (*)
– Biến đổi phương trình về dạng: f(x) = g(m).
– Số nghiệm của phương trình (*) là số giao điểm của (C ): y = f(x) và đường thẳng (d): y = g(m) (d là đường thẳng cùng phương Ox)
– Dựa vào đồ thị để biện luận.
Ví dụ 2: Cho hàm số y=(2x-3)/(x-1) có đồ thị hàm số (H). Tìm m để đường thẳng d: x+3y+m=0 cắt (H) tại hai điểm M, N sao cho tam giác AMN vuông tại điểm A(1;0)
* Lời giải: Ta có d: y=(-1/3)x-(m/3)
Hoành độ giao điểm của d và (H) là nghiệm của phương trình:
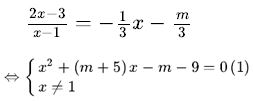
Để (H) cắt d tại hai điểm phân biệt thì:
Ta thấy hệ trên đúng với mọi m.
Do đó d luôn cắt (H) tại 2 điểm phân biệt M(x1,y1); N(x2,y2) ta có:
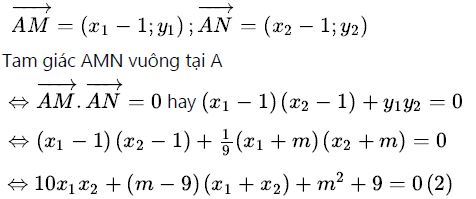
Áp dụng định lý Viet, ta có: x1+x2=-m-5; x1x2= -m-9
Thay vào (2) ta được : 10 (−m − 9) + (m − 9) (−m − 5) + m2 + 9 = 0 <=> −6m − 36 = 0 <=>m=-6
Kết luận: m=-6 là giá trị cần tìm
* Bài toán 3: Phương trình tiếp tuyến của đồ thị hàm số
Cho hàm số y = f(x) có đồ thị (C)
+ Hệ số góc của tiếp tuyến với (C) tại điểm M(x0; y0) Î (C) là : k = y’(x0)
+ PT tiếp tuyến của (C) tại điểm M(x0,y0) (C ) có dạng: y = f’(x0)(x-x0)+ y0
* Chú ý:
+ Tiếp tuyến song song với (d): y = ax + b có hệ số góc k = a.
+ Tiếp tuyến vuông góc với (d): y = ax + b có hệ số góc k = -1/a
– Một số ví dụ viết phương trình tiếp tuyến của đồ thị hàm số sau:
Ví dụ 3: Cho hàm số y=x3 – 6×2 + 9x có đồ thị (C). Hãy viết phương trình tiếp tuyến tại điểm M(2,2) ∈(C).
* Lời giải: Ta có y’=3×2 – 12x + 0 với x=2 thì y'(2)=-3
Phương trình tiếp tuyến với đồ thị (C) tại điểm A(2,2) là: y = (-3)(x-2)+2 = -3x+8
Ví dụ 4: Cho hàm số y=x3 + 3×2 – 1 có đồ thi (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là -1.
Lời giải: Ta có hoành độ tiếp điểm x = -2 thì y =1 và y’ = 2×2 + 6x ⇒ y'(-1)=-3
Phương trình tiếp tuyến của đồ thị hàm số tại (-1,1) là y = (-3)(x+1) + 1 = -3x – 2
Ví dụ 5: Cho hàm số y = x3 – 3×2 có đồ thì (C). Viết phương trình tiếp tuyến đồ thị (C) biết hệ số góc của tiếp tuyến k = – 3.
* Lời giải: Ta có y’ = 3×2-6x
Tìm tọa độ tiếp điểm: y’=k ⇔ 3×2 – 6x = -3 ⇔ x = 1 ⇒ y = -2
Phương trình tiếp tuyến tại (1,-2) có hệ số góc k=-3 có dạng: y=(-3)(x-1)-2 = -3x + 1
>> có thể bạn muốn xem:
- Ứng dụng đạo hàm, Khảo sát hàm số
