Nội dung bài viết
Hình học với nhiều các loại đường thẳng khác nhau: đường trung trực, đường trung tuyến,…. Liệu rằng bạn đã nắm rõ hết được những đường thẳng đó hay chưa? Trong bài viết này, các bạn hãy cùng Studytienganh.vn tìm hiểu về tính chất đường trung tuyến trong tam giác vuông và một số bài tập minh họa về đường trung tuyến nhé!
1. Đường trung tuyến là gì?
Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC. Đôi khi, đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.
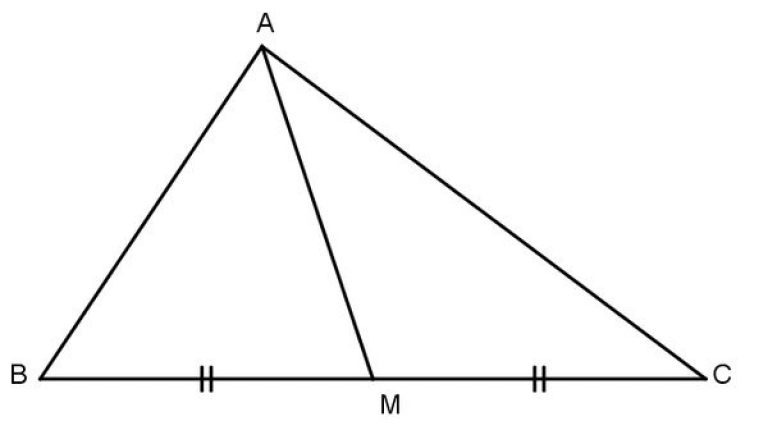
( Hình ảnh minh họa về đường trung tuyến trong hình học )
– Mỗi tam giác có ba đường trung tuyến.
2. Một số định lý đường trung tuyến trong tam giác
- Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. điểm gặp nhau của 3 đường trung tuyến gọi là trọng tâm của tam giác đó.
- Định lý 2: Đường trung tuyến của tam giác chia tam giác ấy thành hai tam giác có diện tích bằng nhau. Ba trung tuyến chia tam giác thành 6 tam giác nhỏ với diện tích bằng nhau.
Chứng minh định lý:
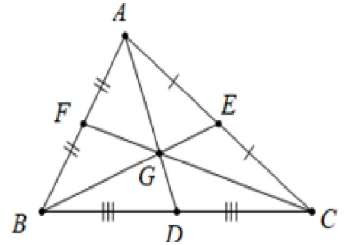
( Hình ảnh về 3 đường trung tuyến trong tam giác )
Tam giác ΔABC có D, E, F là BC, CA, AB. Khi đó AD, BE, CF lần lượt là các đường trung tuyến xuất phát từ ba đỉnh A, B, C. AD, BE, CF đồng quy ở G.
Ta có G là trọng tâm của tam giác ΔABC.
Theo định nghĩa, AE = EC, CD = DB, BF = FA, do đó:
SΔAGE = SΔCGE; SΔBGD = SΔCGD; SΔAGF = SΔBGF trong đó kí hiệu SΔABC là diện tích của tam giác ABC.
Điều này đúng bởi trong mỗi trường hợp hai tam giác có chiều dài đáy bằng nhau, và có cùng đường cao từ đáy, mà diện tích của một tam giác thì bằng ½ chiều dài đáy nhân với đường cao, khi ấy hai tam giác ấy có diện tích bằng nhau.
Chúng ta có:
SΔACG = SΔACD − SΔCGD; SΔABG = SΔABD − SΔBGD
Do đó ta có :SΔABG = SΔACG và SΔDBG = SΔDCG; SΔCDG = ½SΔACG
Do SΔBGF = SΔAGF, SΔAGF = ½SΔACG = SΔBGF = ½SΔBCG
Do vậy, SΔAFG=SΔBFG=SΔBGD=SΔCGD
Từ đó ta có kết quả sau:
SΔAFG=SΔBFG=SΔBGD=SΔCGD=SΔCGE=SΔAGE
- Định lý 3: Vị trí trọng tâm trong tam giác: Trọng tâm của 1 tam giác cách mỗi đỉnh 1 khoảng bằng độ dài đường trung tuyến đi qua đỉnh đó.
Chứng minh định lý:
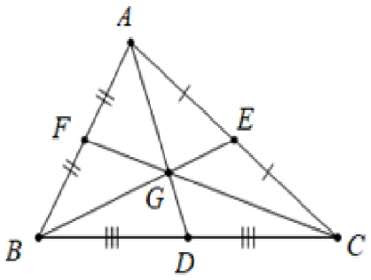
( Hình ảnh minh họa 3 đường trung tuyến trong tam giác )
Tam giác ΔABC có AD, BE, CF lần lượt là các đường trung tuyến xuất phát từ ba đỉnh A, B, C. Theo định lý 1 thì ba đường này đồng quy tại một điểm gọi là điểm G.
Theo định lý 2 thì:
AG=⅔ AD; BG=⅔ BE; CG=⅔ CF
3. Tính chất của đường trung tuyến tam giác vuông
- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
- Một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.
ABC vuông có AD là trung tuyến ứng với cạnh huyền BC.
=> AD = 1/2BC = DB = DC
Ngược lại, nếu trung tuyến AM = 1/2BC thì ABC vuông tại A.
4. Tính chất của đường trung tuyến trong tam giác cân và vuông cân
Trong tam giác cân
+ Tính chất 1: Đường trung tuyến ứng từ góc đỉnh sẽ vuông góc với cạnh đáy tương ứng (đường trung trực của cạnh đáy)
+ Tính chất 2: Đường trung tuyến ứng từ góc đỉnh sẽ chia góc đỉnh thành 2 góc bằng nhau (đường phân giác của góc đỉnh).
+ Tính chất 3: Có đủ các tính chất của tam giác thường.
Trong tam giác đều
+ Tính chất 1: Ba đường trung tuyến của tam giác đều có độ dài bằng nhau.
+ Tính chất 2: Ba đường trung tuyến đồng thời cũng là 3 đường phân giác và đường trung trực của tam giác đều.
+ Tính chất 3: Có đầy đủ các tính chất của đường trung tuyến tam giác cân.
Trong tam giác vuông cân
Tam giác vuông cân là một tam giác có một góc vuông với hai cạnh góc vuông bằng nhau và bằng a. Từ đó, trung tuyến trong tam giác vuông cân mà nối từ góc vuông đến cạnh đối diện sẽ là một đoạn thẳng vuông góc với cạnh huyền và bằng một phần hai nó.
5. Một số bài tập vận dụng
Câu 1: Cho tam giác ABC cân ,biết AB=AC=10cm, BC=12cm, điểm M là trung điểm của BC. Tính độ dài đường trung tuyến AM?
A. 25cm
B. 22cm
C. 5cm
D. 8cm
Đáp án: D
Câu 2: Cho tam giác ABC có trung tuyến AM = 9cm và G là trọng tâm. Độ dài của đoạn thẳng AG là:
A. 5,5cm
B. 9cm
C. 6cm
D. 14cm
Đáp án: C.
Câu 3: Cho tam giác ABC có hai đường trung tuyến BM và CN. Nếu BM = CN thì ΔABC là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác vuông cân
D. Tam giác đều
Đáp án: B
Câu 4: Cho ΔABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME = MG. Kéo dài CN lấy đoạn NF=NG. Chứng minh:
a) EF=BC
b) Đường thẳng AG đi qua trung điểm BC.
Cách giải:
a) Ta có BM và CN là hai đường trung tuyến gặp nhau tại G nên G là trọng tâm của tam giác ΔABC.
⇒ GC = 2GN
mà FG = 2GN ⇒ GC=GF
Tương tự BG, GE và ∠G1 = ∠G2 (đd). Do đó ΔBGC = ΔEGF(c.g.c))
Suy ra BC = EF.
b.) G là trọng tâm nên AG chính là đường trung tuyến thứ ba trong tam giác ABC nên AG đi qua trung điểm của BC.
Trên đây là những kiến thức về tính chất đường trung tuyến trong tam giác vuông. Studytienganh.vn mong rằng với bài viết này, các bạn có thể trang bị cho mình những kỹ năng về toán học thật bổ ích và hiệu quả.






