Phân tích đa thức thành nhân tử là dạng bài thường gặp trong chương trình Toán lớp 8 phần Đại số. Vì vậy học sinh 2k7 cần chú trọng học tốt phần kiến thức này để giải các dạng toán liên quan.
Phân tích đa thức thành nhân tử là dạng bài tương đối khó trong chương trình Toán lớp 8 phần Đại số. Ngoài ra, đây còn là kiến thức nền tảng để học sinh học những nội dung tiếp theo vì vậy cần đặc biệt lưu ý trong quá trình học để không bị mất gốc kiến thức.
Để giải quyết dạng bài phân tích đa thức thành nhân tử trong Toán lớp 8, học sinh hãy theo dõi ngay những hướng dẫn của thầy Bùi Minh Mẫn – Giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI trong bài viết dưới đây. Theo đó thầy sẽ đưa ra cho học sinh 6 các cách phân tích đa thức thành nhân tử thông dụng cần ghi nhớ và các ví dụ cụ thể đối với từng phương pháp để học sinh biết cách vận dụng lí thuyết vào làm bài tập.
I. Phương pháp phân tích đa thức thành nhân tử
Phương pháp 1: Đặt nhân tử chung
– Trong đa thức có nhiều hạng tử, ta tìm xem chúng có nhân tử chung là gì.
– Phân tích mỗi hạng tử thành tích của nhân tử chung và nhân tử khác.
– Đặt nhân tử chung ra ngoài, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng).
Ví dụ: Phân tích đa thức thành nhân tử:
Phương pháp 2: Phương pháp dùng hằng đẳng thức
Ở phương pháp này, ta vận dụng các hằng đẳng thức để biến đổi đa thức thành tích các nhân tử hoặc lũy thừa của một đa thức đơn giản.
Ví dụ: Phân tích đa thức thành nhân tử
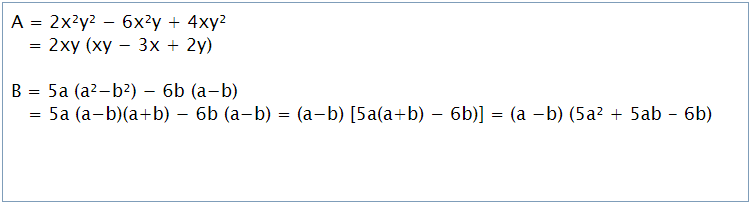
Phương pháp 3: Phương pháp nhóm hạng tử
– Ta xem trong đa thức đó, có những hạng tử nào có thể nhóm lại với nhau.
– Sau đó phân tích chúng thành các đơn thức, đa thức đơn giản hơn.
– Đặt thừa số chung, có thể sử dụng hằng đẳng thức để phân tích.
Ví dụ: Phân tích đa thức thành nhân tử
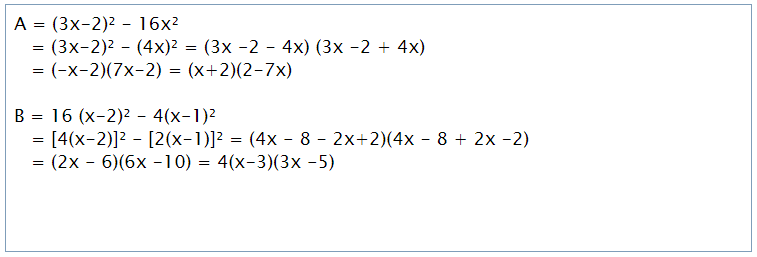
Phương pháp 4: Phương pháp tách hạng tử
Ví dụ: Phân tích đa thức thành nhân tử
Phương pháp 5: Phương pháp thêm, bớt hạng tử
Ví dụ: Phân tích các đa thức sau thành nhân tử
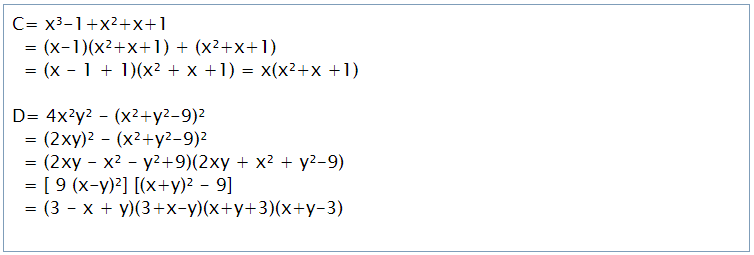
Phương pháp 6: Phương pháp đặt ẩn phụ
Ví dụ: Phân tích các đa thức sau thành nhân tử
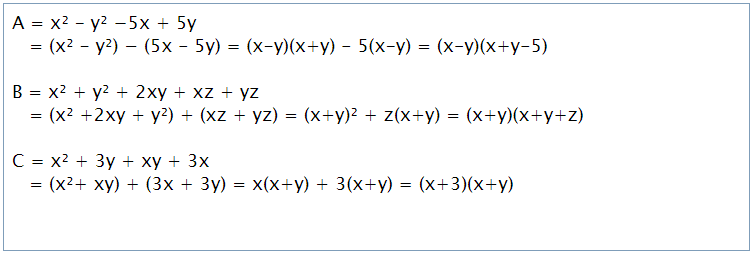
Phương pháp 7: Giảm dần số mũ của lũy thừa
Phương pháp 8: Sử dụng phương pháp hệ số bất định
II. Bài tập vận dụng phương pháp phân tích đa thức thành nhân tử
Bài tập số 1: Phân tích các đa thức sau đây thành nhân tử
a) x2 – y2 – 3x + 3y
b) 2x + 2y – x2 + y2
c) x2 – 16 + y2 + 2xy
d) x2 – 2x – 9y2 – 9y
e) x2y – x3 – 10y + 10x
f) x2(x -2) + 49(2- x)
Bài tập số 2: Phân tích các đa thức sau đây thành nhân tử
a) 4×2 – 16 + (3x + 12)(4 – 2x)
b) x3 + x2y – 15x – 15y
c) 3(x+ 8) – x2 – 8x
d) x3 – 3×2 + 1 – 3x
e) 5×2 – 5y2 – 20x + 20y
f) 3×2 – 6xy + 3y2 – 12z2
g) x2 – xy + x – y
h) x2 – 2x – 15
Bài tập số 3: Phân tích các đa thức sau đây thành nhân tử
a) 2×2 + 3x – 5
b) x2 + 4x – y2 + 4
c) 2×2 – 18
d) x3 – x2 – x + 1
e) x2 – 7xy + 10y2
f) x4 + 6x2y + 9y2 – 1
g) x3 – 2×2 + x – xy2
h) ax – bx – a2 + 2ab – b2
Bài tập số 4: Phân tích các đa thức sau đây thành nhân tử
a) x4y4 + 4
b) x7 + x2 + 1
c) x4y4 + 64
d) x8 + x + 1
e) x8 + x7 + 1
f) 32×4 + 1
g) x8 + 3×4 + 1
h) x4 + 4y4
i) x10 + x5 + 1
Bài tập số 5: Phân tích các đa thức sau đây thành nhân tử
a) x2 + 2xy – 8y2 + 2xz + 14yz – 3z2
b) 3×2 – 22xy – 4x + 8y + 7y2 + 1
c) 12×2 + 5x – 12y2 + 12y – 10xy – 3
d) 2×2 – 7xy + 3y2 + 5xz – 5yz + 2z2
e) x2 + 3xy + 2y2 + 3xz + 5yz + 2z2
f) x2 – 8xy + 15y2 + 2x – 4y – 3
g) x4 – 13×2 + 36
h) x4 + 3×2 – 2x + 3
i) x4 + 2×3 + 3×2 + 2x + 1
Bài tập số 6: Phân tích các đa thức sau đây thành nhân tử
a) (a – b)3 + (b – c)3 + (c – a)3
b) (a – x)y3 – (a – y)x3 – (x – y)a3
c) x(y2 – z2) + y(z2 – x2) + z(x2 – y2)
d) (x + y + z)3 – x3 – y3 – z3
e) 3×5 – 10×4 – 8×3 – 3×2 + 10x + 8
f) 5×4 + 24×3 – 15×2 – 118x + 24
g) 15×3 + 29×2 – 8x – 12
h) x4 – 6×3 + 7×2 + 6x – 8
i) x3 + 9×2 + 26x + 24
Bài tập số 7: Phân tích các đa thức sau đây thành nhân tử
a) (x2 + x)2 + 4×2 + 4x – 12
b) (x2 + 4x + 8)2 + 3x(x2 + 4x + 8) + 2×2
c) (x2 + x + 1)(x2 + x + 2) – 12
d) (x + 1)(x + 2)(x + 3)(x + 4) – 24
e) (x2 + 2x)2 + 9×2 + 18x + 20
f) x2 – 4xy + 4y2 – 2x + 4y – 35
g) (x + 2)(x + 4)(x + 6)(x + 8) + 16
h) (x2 + x)2 + 4(x2 + x) – 12
i) 4(x2 + 15x + 50) – (x2 + 18x + 74) – 3×2
Trên đây là tổng hợp các kiến thức chuyên đề phương pháp phân tích đa thức thành nhân tử thường gặp trong môn Toán lớp 8. Thông qua những nội dung thầy Bùi Minh Mẫn chia sẻ, hy vọng học sinh sẽ làm bài tập dạng này một cách hiệu quả nhất.
Ngoài ra, để học tốt môn Toán lớp 8, tạo tiền đề để bứt phá điểm số trong bài thi cuối học kỳ I sắp tới, học sinh 2K7 hãy tham khảo ngay Chương trình Học tốt 2022-2023 của HOCMAI.
Chương trình được thiết kế với lộ trình học bài bản từ học lý thuyết qua các video bài giảng đến vận dụng kiến thức qua các bài tập tự luyện sẽ giúp học sinh tiếp thu bài học hiệu quả ngay tại nhà mà không cần phải vất vả đi học thêm bên ngoài. Đặc biệt với những phần kiến thức không hiểu học sinh có thể xem lại video bài giảng để thấm nhuần kiến thức hoặc để lại thắc mắc dưới bài giảng để được đội ngũ trợ giảng hỗ trợ giải đáp
