Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Khối đa diện Toán lớp 12, tài liệu bao gồm 4 trang, tuyển chọn 9 bài tập Khối đa diện đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Khối đa diện – Hình học lớp 12 gồm các nội dung chính sau:
I. Phương pháp giải
– Tổng hợp lý thuyết trọng tâm
II. Ví dụ minh họa
– Gồm 9 ví dụ minh họa đa dạng của các dạng bài tập có lời giải chi tiết.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Bài giảng Toán 12 Bài 1: Khái niệm về khối đa diện
I. Phương pháp giải
– Hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:
(1) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
(2) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
– Hình đa diện chia không gian làm hai phần: phần bên trong và phần bên ngoài. Hình đa diện cùng với phần bên trong của nó gọi là khối đa diện.
– Mỗi khối đa diện có thể phân chia được thành những khối tứ diện.
Mỗi đa giác của hình H được gọi là một cặp của khối đa diện. Các đỉnh, các cạnh của mỗi mặt còn gọi là đỉnh, cạnh của khối đa diện. Các điểm nằm trong hình H còn gọi là điểm trong của khối đa diện.
– Khối đa diện được gọi là khối chóp, khối chóp cụt nếu nó được giới hạn bởi một hình chóp, hình chóp cụt. Tương tự cho khối chóp n-giác, khối chóp cụt n-giác, khối chóp đều, khối tứ diện.
– Khối đa diện được gọi là khối lăng trụ nếu nó được giới hạn bởi một hình lăng trụ, tương tự cho khối hộp, khối hộp chữ nhật, khối lập phương,…
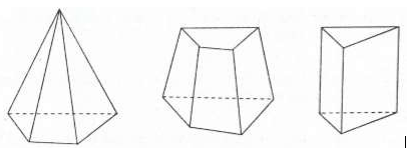
– Phân chia và lắp ghép các khối đa diện: Mọi khối chóp và khối lăng trụ luôn có thể phân chia được thành những khối tứ diện bằng nhiều cách khác nhau.
1) Đặc số Ơ-le của khối đa diện lồi: Đối với mỗi khối đa diện lồi H, ta kí hiệu Đ là số đỉnh, C là số cạnh, M là số mặt của H thì có đặc số c (H ) = D – C + M = 2
2) Hình lăng trụ đều; hình lăng trụ đứng (có cạnh bên vuông góc với mặt đáy) và có đáy là đa giác đều.
3) Hình chóp đều: đáy là đa giác đều và các cạnh bên bằng nhau.
Xem thêm
