Mệnh đề nằm trong chương mở đầu của sách giáo khoa đại số lớp 10 và để học tốt toán 10 các em cần nắm vững kiến thức ngay từ bài học đầu tiên. Vì vậy trong bài viết này chúng ta sẽ cùng thầy Lưu Huy Thưởng (giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI) ôn lại kiến thức.
Mục lục
I. Mệnh đề 1. Khái niệm mệnh đề 2, Phủ định của một mệnh đề 3, Mệnh đề kéo theo 4. Mệnh đề đảo – Hai mệnh đề tương đương
II. Mệnh đề chứa biến 1. Mệnh đề chứa biến 2. Kí hiệu với mọi, tồn tại 3. Mệnh đề phủ định của mệnh đề có chứa mọi
I. Mệnh đề
1, Khái niệm mệnh đề
Định nghĩa: Mệnh đề là một câu khẳng định đúng hoặc sai.
Chú ý: Những câu nghi vấn và cảm thán thường không phải là mệnh đề. Một mệnh đề không thể vừa đúng vừa sai
Ví dụ: 
2, Phủ định của một mệnh đề
Cho mệnh đề P, mệnh đề không phải P được gọi là mệnh đề phủ định của P.
Kí hiệu:
Ví dụ: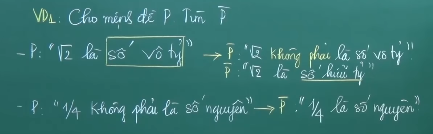 
3, Mệnh đề kéo theo
Mệnh đề có dạng: “Nếu P thì Q” được gọi là mệnh đề kéo theo.
Kí hiệu:
Ví dụ: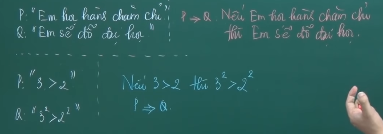 
Vậy khi nào mệnh đề này là đúng, mệnh đề kia là sai? Để phân biệt tính đúng sai của mệnh đề ta có bảng sau:
Chú ý: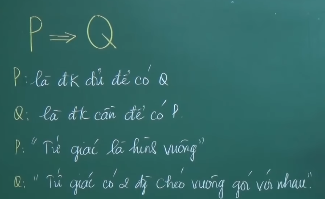
Điều kiện đủ là khi P xảy ra thì chắc chắn có Q. Điều kiện cần là khi Q xảy ra thì chưa chắc P xảy ra.
4. Mệnh đề đảo – Hai mệnh đề tương đương
a, Mệnh đề đảo
Cho mệnh đề kéo theo P ⇒ Q
Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q
P ⇒ Q: “Nếu P thì Q” thì mệnh đề đảo là Q ⇒ P: “Nếu Q thì P”
Ví dụ:
P: “Tứ giác là hình bình hành”
Q: “Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường”
b, Hai mệnh đề tương đương
Cho hai mệnh đề P và Q. Mệnh đề có dạng “P nếu và chỉ nếu Q” hoặc “P khi và chỉ khi Q” được gọi là mệnh đề tương đương.
Kí hiệu: P ⟺ Q
Cách xét đúng sai của hai mệnh đề: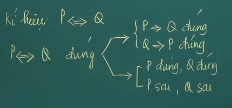 
Ví dụ: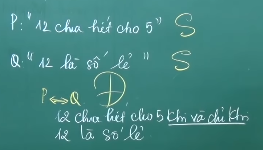 
Chú ý: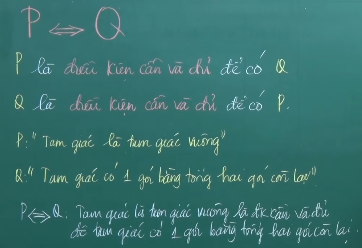 
II. Mệnh đề chứa biến
1. Mệnh đề chứa biến
Xét câu “n chia hết cho 3”
n=1 ⇒ “1 chia hết cho 3” là mệnh đề sai
n=9 ⇒ “9 chia hết cho 3” là mệnh đề đúng
Những câu khẳng định mang tính chất đúng sai phụ thuộc vào biến được gọi là mệnh đề chứa biến.
Ví dụ: 
2. Kí hiệu với mọi, tồn tại
a. Kí hiệu với mọi
Cho mệnh đề chứa biến P(x) với x thuộc X
Khẳng định: “Với mọi x thuộc X, P(x) đúng” hay “P(x) đúng với mọi x thuộc X” là một mệnh đề
Kí hiệu: Ví dụ: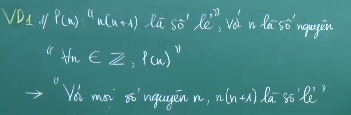 
Xét tính đúng sai:
b. Kí hiệu tồn tại
Cho mệnh đề chứa biến P(x) với x thuộc X
Khẳng định: “Tồn tại x thuộc X, P(x) đúng” là một mệnh đề
Kí hiệu:
Ví dụ: 
Xét tính đúng sai: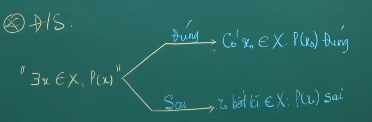 
3. Mệnh đề phủ định của mệnh đề có chứa mọi
Cho mệnh đề chứa biến P(x) với x thuộc X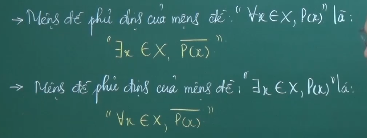 
Ví dụ: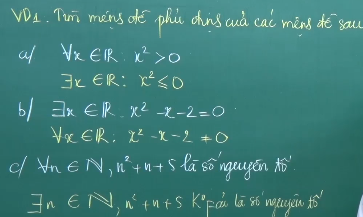 
Hy vọng với bài viết kèm video giảng dạy của thầy Lưu Huy Thưởng về mệnh đề và mệnh đề chứa biến sẽ giúp ích cho các em trong quá trình nhập môn đại số 10.
