Nội dung bài viết
Trong toán học chúng ta thấy hình vuông là một trong các nội dung rất quan trọng và ứng dụng rất nhiều trong thực tế cuộc sống. Chính vì thế nên Công thức tính diện tích hình vuông, tính chu vi hình vuông cũng được sử dụng rất nhiều trong học tập và thực tế thông qua đó tính toán các số liệu được chuẩn hơn.
Tư vấn pháp luật trực tuyến miễn phí qua tổng đài: 1900.6568
1. Công thức tính diện tích hình vuông, tính chu vi hình vuông:
1.1. Công thức tính diện tích hình vuông:
Như chúng ta đã biết thì hình vuông là hình tứ giác có 4 cạnh và 4 góc bằng nhau:
Cách tính diện tích hình vuông: S = a x a hoặc S = a2
+ a : Độ cài của một cạnh bất kỳ trong hình vuông
+ S: Diện tích hình vuông
Giống như cách tính chu vi hình vuông, bài toán áp dụng công thức tính diện tích hình vuông cũng khá dễ thực hiện khi người giải biết được các con số cần thiết.
– Ví dụ:
VD1: Cho hình vuông ABCD có cạnh bằng 6cm. Tính diện tích hình vuông.
Giải: Áp dụng công thức, ta có diện tích hình vuông có cạnh 6cm là 6 x 6 = 36cm2.
Đáp án: 36cm2.
VD2: Cho một hình vuông ABCD chiều dài các cạnh bằng nhau và bằng 4 cm. Hỏi diện tích của hình vuông ABCD bằng bao nhiêu?
Giải:
Theo công thức tính diện tích hình vuông ở trên, bạn đọc có thể áp dụng để tính diện tích hình vuông ABCD trong bài toán dễ dàng.
Có chiều dài các cạnh a=b=c=d= 4cm. Như vậy khi ứng dụng vào cách tính diện tích hình vuông, ta có:
S = a x a = 4 x 4 = 16 cm2
Công thức tính diện tích hình vuông khi biết đường chéo
Hình vuông cũng là hình thoi. Do đó, nếu biết được hai đường chéo hình vuông, bạn có thể áp dụng công thức tính diện tích hình thoi vào bài tập hình vuông này.
S = 1/2 (d1 x d2)
Trong đó:
– S là diện tích.
– d1, d2: lần lượt là đường chéo hình vuông.
1.2. Công thức tính chu vi hình vuông:
– Khái niệm tính chu vi hình vuông: Chu vi hình vuông là tổng độ dài bốn cạnh của nó hay gấp bốn lần độ dài của một cạnh.
Công thức tính chu vi hình vuông: P = a x 4
Trong đó:
+ a : độ cài của một cạnh bất kỳ trong hình vuông
+ P: Chu vi hình vuông
– Ví dụ: Có một hình vuông ABCD có chiều dài các cạnh bằng nhau và bằng 5cm. Yêu cầu tính chu vi hình vuông ABCD?
Giải: Áp dụng theo công thức tính chu vi hình vuông ở trên, ta có các cạnh a=b=c=d =5 cm. Như vậy khi đưa vào công thức tính chu vi hình vuông, ta có:
P = 5 x 4 = 20 cm
(Lưu ý: Công thức tính chu vi, tính diện tích hình vuông này đều áp dụng cho tất cả các khối lớp, từ lớp 3, lớp 4 trở đi)
Hình vuông là một hình tứ giác có 4 góc bằng nhau và bằng 90 độ, có các cạnh bằng nhau. Tính chất của hình thoi, hình chữ nhật, hình thang đều có ở hình vuông.
Tính chất hình vuông: Hình vuông có đủ tính chất của các hình chữ nhật, hình thoi …
Dấu hiệu nhận biết hình vuông:
– Hình thoi có 1 góc vuông
– Hình thoi có hai đường chéo bằng nhau
– Hình chữ nhật có một đường chéo là phân giác của góc hình chữ nhật
– Hình chữ nhật có hai đường chéo vuông góc với nhau
– Hình chữ nhật có hai cạnh kề bằng nhau
2. Lưu Ý Về Diện Tích, Chu Vi Của Hình Vuông:
Để không bị mất điểm khi làm bài kiểm tra, bài thi cũng như làm bài tập chính xác, bên cạnh áp dụng cách tính, công thức tính diện tích, chu vi, bạn nên chú ý tới đơn vị đo.
– Với diện tích, đơn vị đo lường mũ 2 như m2, cm2.
– Với chu vi, đơn vị đo lường như bình thường theo đề bài đưa ra.
Như vậy từ những phân tích như trên ta thấy được hình vuông là một hình học khá quen thuộc trong toán học và cụ thể là môn hình học. Trả lời câu hỏi hình vuông là gì hay nói cách khác xác định những dấu hiệu để nhận biết về hình vuông. Hình vuông trước hết là một tứ giác có 4 cạnh. Tuy nhiên, hình vuông khác với các hình còn lại là hình vuông có 4 cạnh bằng nhau. Đồng thời hình vuông có 4 góc vuông và các cặp cạnh đối diện song song và bằng nhau.
3. Bài Tập Về Diện Tích, Chu Vi Hình Vuông:
Bài 1: Cho hình vuông ABCD có chu vi bằng 28cm. Tính diện tích hình vuông ABCD.
Giải:
– Ta có, cạnh AB = BC = CD = DA = 28 : 4 = 7 cm – Diện tích hình vuông ABCD = 7 x 7 = 49 cm2
Bài 2: Tính diện tích hình vuông có chu vi là 32cm.
Giải – Ta có, chu vi hình vuông là 32, nên các cạnh hình vuông là 32 : 4 = 8 cm.
– Diện tích hình vuông là 8 x 8 = 64 cm2
Như vậy, diện tích hình vuông có chu vi là 32cm là 64cm2.
Bài 3: Một miếng đất hình vuông được mở rộng về 1 phía là 5cm thì ta có được chu vi hình chữ nhật là 110m. Sau khi mở rộng diện tích, tính miếng đất có diện tích.
Cạnh miếng đất hình vuông là 100 : 4 = 25 cm
Chiều dài miếng đất của hình chữ nhật là: 25 + 8 = 33 cm
Sau khi mở rộng thì diện tích miếng đất là 25 x 33 = 825cm2
II. Các dạng toán và phương pháp giải
Dạng 1: Chứng minh tứ giác là hình vuông
Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông.
Ví dụ: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh tứ giác EFGH là hình vuông.
Lời giải:
Vì ABCD là hình vuông nên AB = BC = CD = DA và
Ta có:
mà AB = BC = CD = DA và AE = BF = CG = DH
Nên EB = CF = DG = AH
Xét tam giác AHE và tam giác BEF có
AH = BE (chứng minh trên)
AE = BF (giả thuyết)
Do đó: ΔAHE = ΔBEF (c – g – c)
=> HE = EF (hai cạnh tương ứng) (1); (hai góc tương ứng)
Xét tam giác CFG và tam giác DGH có
CF = DG (chứng minh trên)
CG = DH (giả thiết)
Do đó: ΔCFG = ΔDHG (c – g – c)
=> FG = GH (hai cạnh tương ứng) (2)
Xét tam giác CFG và tam giác AHE có
CF = AH(chứng minh trên)
CG = AE (giả thiết)
Do đó: ΔCFG = ΔAHE (c – g – c)
=> FG = HE (hai cạnh tương ứng) (3)
Xét tứ giác EFGH ta có:
FG = HE = GH = EF (theo (1), (2), (3))
Nên tứ giác EFGH là hình thoi
Lại có:
(do tam giác vuông)
Mà (chứng minh trên)
Nên
Mặt khác:
Mà hình thoi EFGH có một góc vuông nên hình thoi EFGH là hình vuông.
Dạng 2: Vận dụng tính chất của hình vuông để chứng minh các tính chất hình học
Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình vuông.
Ví dụ: Cho hình vuông ABCD. Trên cạnh AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh:
a) Hai tam giác ADF và BAE bằng nhau;
b) BE vuông góc với AF.
Lời giải:
a) Vì ABCD là hình vuông nên AB = AD và
Xét hai tam giác ADF và BAE ta có:
AD = AB
AE = DF ( giả thiết)
Do đó: ΔADF = ΔBAE (c – g – c)
b) Gọi giao điểm của BE và AF là G.
Ta có:
Mà ( hai góc tương ứng của hai tam giác bằng nhau ΔADF = ΔBAE )
Nên
Mà theo định lý tổng ba góc trong tam giác AEG ta có:
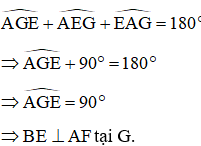
Dạng 3: Tìm điều kiện để tứ giác là hình vuông
Phương pháp giải: Vận dụng định nghĩa và các tính chất và dấu hiệu nhận biết của hình vuông.
Ví dụ: Cho tam giác ABC vuông cân tại A, M là một điểm thuộc cạnh BC. Qua M vẽ các đường thẳng song song với AC, AB chúng cắt các cạnh AB, AC theo thứ tự tại E và F.
a) Tứ giác AFME là hình gì?
b) Xác định vị trí điểm M trên cạnh BC để tứ giác AFME là hình vuông.
Lời giải
a) Ta có tam giác ABC vuông tại A nên AB ⊥ AC
Vì MF // AB nên MF ⊥ AC =>
Vì ME // AC nên ME ⊥ AB =>
Xét tứ giác AFME có:
Do đó tứ giác AFME là hình chữ nhật.
b) Để tứ giác AFME là hình vuông thì MF = ME (hình chữ nhật có hai cạnh kề bằng nhau).
Ta có: (do tam giác ABC cân tại A)
Mà (tam giác MEB vuông tại E); (tam giác FMC vuông tại F)
Suy ra
Xét tam giác MFC và tam giác MEB có
MF = ME (giả thuyết hình vuông)
Do đó: ΔMFC = ΔMEB (cạnh góc vuông và góc nhọn kề nó)
=> MB = MC (hai cạnh tương ứng) hay M là trung điểm của BC.
III. Bài tập tự luyên
Bài 1: Cho hình vuông ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF.
a) Chứng minh tam giác EDF vuông cân.
b) Gọi I là trung điểm của EF. Chứng minh BI = DI.
c) Chứng minh A, C, I thẳng hàng.
Bài 2: Cho tứ giác ABCD. Gọi E, F, G, H theo thứu tự là trung điểm của AB, BC, CD, AD. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là
a) Hình chữ nhật;
b) Hình thoi;
c) Hình vuông.
Trên đây là những hướng dẫn về cách tính diện tích hình vuông, chu vi hình vuông, công thức tính, hi vọng qua bài viết các bạn đã hiểu rõ hơn về cách tính, công thức tính diện tích hình vuông, chu vi hình vuông và áp dụng vào các bài toán thực tế.
Các bạn cũng có thể tham khảo thêm về cách tính diện tích hình thoi, chu vi hình thoi, công thức tính, ngoài hình vuông thì hình thoi cũng là một hình quan trọng, nó mang đầy đủ các tính chất của hình bình hành, công thức tính diện tích hình thoi, chu vi hình thoi dễ nhớ, dễ học sẽ giúp bạn giải quyết những bài toán liên quan đến loại hình này.






