Trọng tâm là gì? Các tính chất của trọng tâm tam giác, hình thang, tứ diện

Trọng tâm là gì?

Trọng tâm là giao điểm của 3 đường trung tuyến xuất phát từ 3 đỉnh trong tam giác

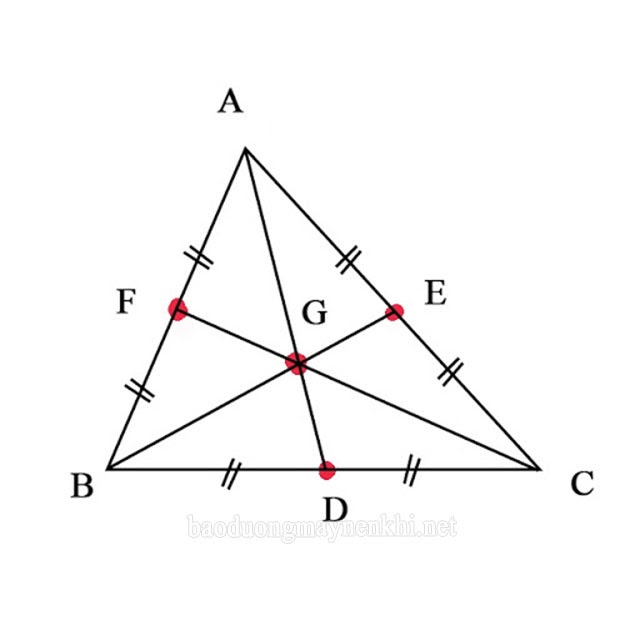
Cho tam giác ABC, trong đó AD, BE, CF lần lượt là trung tuyến của tam giác xuất phát từ đỉnh A, B, C. AD, BE, CF cắt nhau tại G nên G chính là trọng tâm của tam giác

Cách xác định trọng tâm của tam giác

Từ tính chất trọng tâm trong tam giác, ta có 2 cách để xác định trọng tâm của một tam giác. Lấy ví dụ tam giác ABC với 3 đường trung tuyến AD, BE, CF và G là trọng tâm tam giác ABC.

Cách 1:

• Xác định trung điểm D của cạnh BC sao cho D chia BC thành 2 đoạn bằng nhau DC = DB
• Nối đỉnh A với trung điểm D, ta có đường trung tuyến AD
• Thực hiện xác định trung điểm và nối đỉnh tương tự với các trung tuyến khác
• Giao điểm của 3 đường trung tuyến gọi là điểm G. Từ đó, chứng minh được G là trọng tâm ABC.

Cách 2:

• Xác định trung điểm D của cạnh BC sao cho D chia BC thành 2 đoạn bằng nhau DC = DB
• Nối đỉnh A với trung điểm D, ta có đường trung tuyến AD
• Trên trung tuyến AD, chọn điểm G sao cho AG = ⅔ AD
• Dựa trên tính chất trọng tâm tam giác, suy ra G chính là trọng tâm tam giác ABC.

Tính chất trọng tâm

Khoảng cách từ trọng tâm tam giác đến 3 đỉnh của hình tam giác bằng 23 độ dài đường trung tuyến tương ứng với đỉnh đó”.

Như trong Hình 1, từ tính chất trọng tâm tam giác, ta có:

AG=2/3AD

Trọng tâm của tam giác đặc biệt

Trọng tâm tam giác vuông

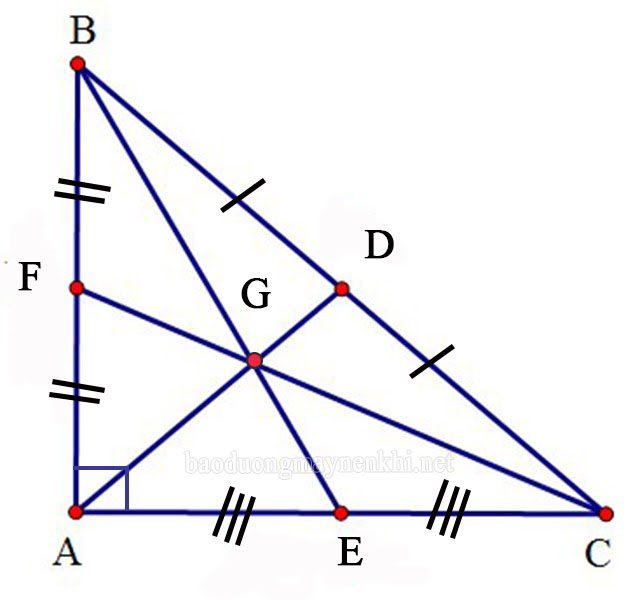
Tam giác ABC vuông tại A, từ A vẽ đường trung tuyến AD, vì AD là đường trung tuyến của góc vuông nên:

AD =BC/2=DB= DC

Vậy tam giác ADB và tam giác ADC lần lượt cân tại D

Trọng tâm tam giác cân

Cho ABC cân tại A, G là trọng tâm ABC. Vì tam giác cân tại A, nên AG vừa là đường trung tuyến, vừa là đường cao và là đường phân giác của ABC.

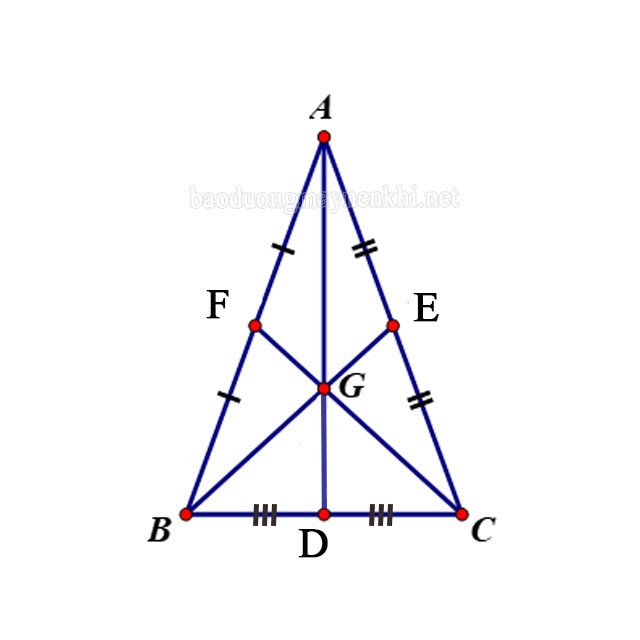
Hệ quả:

Trọng tâm tam giác đều

Cho tam giác ABC đều, G là giao điểm của ba đường trung tuyến. Theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

Trọng tâm của tứ diện

Tính chất trọng tâm của tứ diện

Cho tứ diện ABCD có G là trọng tâm. Khi đó ta có các tính chất sau:

• GA + GB + GC + GD = 0
• G là trung điểm của đường nối 2 trung điểm 2 cạnh đối nhau bất kỳ trong tứ diện.
• G thuộc đường nối một đỉnh của tứ diện với trọng tâm của tam giác đáy tương ứng sao cho khoảng cách từ G đến đỉnh bằng 3 lần khoảng cách từ G đến trọng tâm tam giác đáy.

Cách vẽ trọng tâm của tứ diện

Cách 1

Cho tứ diện ABCD. Khi đó, 3 đường thẳng nối trung điểm 3 cặp cạnh chéo nhau đồng quy tại trung điểm mỗi đường. Điểm đó chính là trọng tâm tứ diện ABCD

Gọi M,N,P,Q lần lượt là trung điểm AB,BC,CD,DA

Khi đó ta có : MQ,NP lần lượt là đường trung bình của ΔABD và ΔCBD

⇒ MQ//NP ( cùng //BD )

⇒ MQ=NP=BD/2

⇒ MNPQ là hình bình hành

⇒ MP∩NQ tại trung điểm mỗi đường

Tương tự chứng minh cặp cạnh chéo nhau còn lại.

Vậy chứng minh được trọng tâm của tứ diện

Cách 2

Cho tứ diện ABCD có G là trọng tâm của ΔBCD. Trên đoạn AG lấy điểm K sao cho KA=3KG. Khi đó điểm K chính là trọng tâm tứ diện ABCD

Ta có:

Vì G là trọng tâm ΔBCD ⇒ GB + GC + GD = 0

KA + KB + KC + KD = KA + (KG + GB) + (KG + GC) + (KG + GD)

= KA + 3KG + (GB + GC + GD)

= KA + 3KG

Mặt khác, vì KA = 3KG ⇒ KA + 3KG = 0

Vậy K là trọng tâm tứ diện ABCD

Trọng tâm hình thang

Lưu ý: Chúng ta không có khái niệm trọng tâm hình thang

Bài toán trọng tâm của các tứ diện đặc biệt

• Tứ diện vuông là tứ diện có đỉnh mà 3 cạnh xuất phát từ đỉnh đó từng đôi một vuông góc với nhau.
• Tứ diện đều là tứ diện có tất cả các cạnh bằng nhau.
• Tứ diện gần đều là tứ diện có các cặp cạnh đối đều bằng nhau.
• Tứ diện trực tâm là tứ diện có các cặp cạnh đối vuông góc với nhau đôi một

Ví dụ: Cho G là trọng tâm của tứ diện vuông OABC ( vuông tại O ). Biết rằng OA=OB=OC=a. Tính độ dài OG

Bài giải

Trên đây là toàn bộ kiến thức cơ bản và mở rộng của phần nội dung kiến thức về trọng tâm là gì. Qua phân tích cùng những ví dụ cụ thể, mong rằng các bạn hiểu được thế nào là trọng tâm và biết áp dụng tính chất của trọng tâm vào từng bài toán cụ thể.